如图,动点 在以 为圆心, 为直径的半圆弧上运动(点 不与点 、 及 的中点 重合),连接 .过点 作 于点 ,以 为边在半圆同侧作正方形 ,过点 作 的切线交射线 于点 ,连接 、 .

(1)探究:如图一,当动点 在 上运动时;
①判断 是否成立?请说明理由;
②设 , 是否为定值?若是,求出该定值,若不是,请说明理由;
③设 , 是否为定值?若是,求出该定值,若不是,请说明理由;
(2)拓展:如图二,当动点 在 上运动时;
分别判断(1)中的三个结论是否保持不变?如有变化,请直接写出正确的结论.(均不必说明理由)
(本小题满分10分)利达经销店为某工厂代销一种建筑材料.当每千克售价为260元时,月销售量为45千克.该经销店为提高经营利润,准备采取降价的方式进行促销.经市场调查发现:当每千克售价下降10元时,月销售量就会增加5千克.综合考虑各种因素,每售出一千克建筑材料共需支付厂家及其它费用100元.设每千克材料售价为x(元),该经销店的月利润为y(元).
(1)当每千克售价是240元时,计算此时的月销售量;
(2)求出y与x的函数关系式(不要求写出x的取值范围);
(3)该经销店要获得最大月利润,售价应定为每千克多少元?
(本小题满分8分)如图,矩形ABCD的对角线AC、BD相交于点O,DE∥AC,CE∥BD.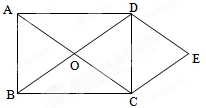
(1)判断四边形OCED的形状,并进行证明;
(2)点E是否在AB的垂直平分线上?若在,请进行证明;若不在,请说明理由.
(本小题满分8分)如图所示,反比例函数y1的图象经过点A(3,2),解答下列问题:
(1)求y1的函数关系式;
(2)过y1上任意一点B向x轴,y轴作垂线,交两坐标轴于C,D两点,求矩形OCBD的面积;
(3)过点A的一次函数y2与反比例函数y1的另一个交点E的横坐标为-1,求y2的关系式;
(4)通过图象回答当x取何值时,y1>y2;
(本小题满分6分)如图,位于A处的海上救援中心获悉:在其北偏东68°方向的B处有一艘渔船遇险,在原地等待营救.该中心立即把消息告知在其北偏东30°且距离A点20海里的C处救生船,此时,遇险船在救生船的正东方向B处,现救生船沿着航线CB前往B处救援,求救生船到达B处行驶的距离?(参考数据:sin68°≈0.90,cos68°≈0.36,tan68°≈2.50,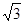 ≈1.7)
≈1.7)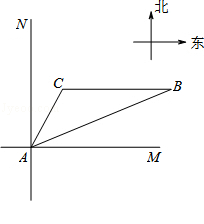
(本小题满分6分)经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,这三种可能性大小相同,现在两辆汽车经过这个十字路口.
(1)请用“树形图”或“列表法”列举出这两辆汽车行驶方向所有可能的结果;
(2)求这两辆汽车都向左转的概率.