垫球是排球队常规训练的重要项目之一．下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩．测试规则为连续接球10个，每垫球到位1个记1分．
运动员甲测试成绩表
测试序号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
成绩（分 |
7 |
6 |
8 |
7 |
7 |
5 |
8 |
7 |
8 |
7 |
（1）写出运动员甲测试成绩的众数和中位数；
（2）在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人，你认为选谁更合适？为什么？（参考数据：三人成绩的方差分别为 、 、
（3）甲、乙、丙三人相互之间进行垫球练习，每个人的球都等可能的传给其他两人，球最先从甲手中传出，第三轮结束时球回到甲手中的概率是多少？（用树状图或列表法解答）
解一元二次方程：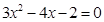 
.
( 
)－1－∣－2∣+2sin30º +(
)º
计算：
如图① ，在△ABC中，AB=AC=4，∠BAC=90ｏ，AD⊥BC，垂足为D.
（1）S△ABD =.(直接写出结果)
（2）如图②，将△ABD绕点D按顺时针方向旋转得到△A′B′D，设旋转角为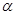
(
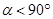)，在旋转过程中：
探究一：四边形APDQ的面积是否随旋转而变化？说明理由
探究二：当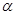的度数为多少时，四边形APDQ是正方形？说明理由.
如图，∠MON＝90°，AP平分∠MAB，BP平分∠ABN．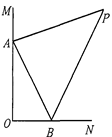
（1）求∠P的度数；
（2）若∠MON＝80°，其余条件不变，求∠P的度数；
（3）经过（1）、（2）的计算，猜想并证明∠MON与∠P的关系．