在平面直角坐标系中,将一点(横坐标与纵坐标不相等)的横坐标与纵坐标互换后得到的点叫这一点的“互换点”,如 与 是一对“互换点”.
(1)任意一对“互换点”能否都在一个反比例函数的图象上?为什么?
(2) 、 是一对“互换点”,若点 的坐标为 ,求直线 的表达式(用含 、 的代数式表示);
(3)在抛物线 的图象上有一对“互换点” 、 ,其中点 在反比例函数 的图象上,直线 经过点 , ,求此抛物线的表达式.
如图,△ABC中,BE⊥AC,CF⊥AB,垂足分别为E、F,M为BC的中点.
(1)求证:ME=MF.
(2)若∠A=50°,求∠FME的度数.
如图,△ABC中,∠C=90°.
(1)在BC边上作一点P,使得点P到点C的距离与点P到边AB的距离相等(尺规作图,不写作法,保留作图痕迹);
(2)在(1)的条件下,若AC=4,BC=3,求CP的长.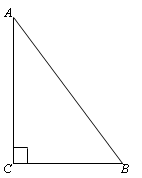
数学家鲁弗斯设计了一个仪器,它可以三等分一个角.如图所示,A、B、C、D分别固定在以O为公共端点的四根木条上,且OA=OB=OC=OD,E、F可以在中间的两根木条上滑动,AE=CE=BF=DF.求证:∠AOE=∠EOF=∠FOD.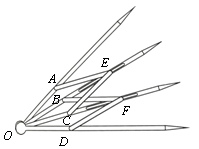
已知:如图,点A、F、C、D在同一直线上,点B和点E分别在直线AD的两侧,且AB=DE,∠A=∠D,AF=DC.求证:△ABC≌△DEF.
有这样的一个定理:夹在两条平行线间的平行线段相等.下面经历探索与应用的过程.
探索:
已知:如图1,AD∥BC,AB∥CD.求证:AB=CD.
应用此定理进行证明求解.
应用一、已知:如图2,AD∥BC,AD<BC,AB=CD.求证:∠B=∠C;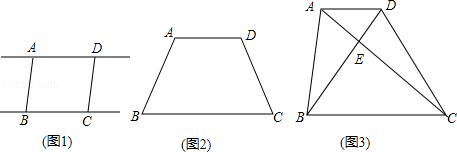
应用二、已知:如图3,AD∥BC,AC⊥BD,AC=4,BD=3.求:AD与BC两条线段的和.