问题背景:已知 的顶点 在 的边 所在直线上(不与 , 重合), 交 所在直线于点 , 交 所在直线于点 ,记 的面积为 , 的面积为 .
(1)初步尝试:如图①,当 是等边三角形, , ,且 , 时,则 ;
(2)类比探究:在(1)的条件下,先将点 沿 平移,使 ,再将 绕点 旋转至如图②所示位置,求 的值;
(3)延伸拓展:当 是等腰三角形时,设 .
(Ⅰ)如图③,当点 在线段 上运动时,设 , ,求 的表达式(结果用 , 和 的三角函数表示).
(Ⅱ)如图④,当点 在 的延长线上运动时,设 , ,直接写出 的表达式,不必写出解答过程.

如图①,在矩形ABCD中,AB=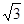 ,BC=3,在BC边上取两点E、F(点E在点F的左边),以EF为边所作等边△PEF,顶点P恰好在AD上,直线PE、PF分别交直线AC于点G、H.
,BC=3,在BC边上取两点E、F(点E在点F的左边),以EF为边所作等边△PEF,顶点P恰好在AD上,直线PE、PF分别交直线AC于点G、H.
(1)求△PEF的边长;
(2)若△PEF的边EF在线段CB上移动,试猜想:PH与BE有何数量关系?并证明你猜想的结论;
(3)若△PEF的边EF在射线CB上移动(分别如图②和图③所示,CF>1,P不与A重合),(2)中的结论还成立吗?若不成立,直接写出你发现的新结论.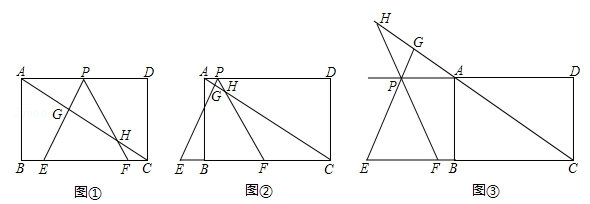
直线y=x+b与双曲线y=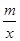 交于点A(﹣1,﹣5).并分别与x轴、y轴交于点C、B.
交于点A(﹣1,﹣5).并分别与x轴、y轴交于点C、B.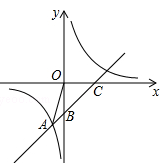
(1)直接写出b= ,m= ;
(2)根据图象直接写出不等式x+b<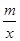 的解集为 ;
的解集为 ;
(3)若点D在x轴的正半轴上,是否存在以点D、C、B构成的三角形与△OAB相似?若存在,请求出D的坐标;若不存在,请说明理由.
如图,在正方形ABCD中,点E、F分别在BC和CD上,AE=AF.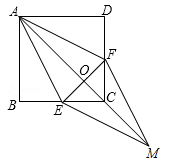
(1)求证:BE=DF
(2)连接AC交EF于点D,延长OC至点M,使OM=OA,连结EM、FM,试证明四边形AEMF是菱形.
如图,一次函数y1=mx+n的图象与x轴、y轴分别交于A、B两点,与反比例函数y2= (x<0)交于点C,过点C分别作x轴、y轴的垂线,垂足分别为点E、F.若OB=2,CF=6,
(x<0)交于点C,过点C分别作x轴、y轴的垂线,垂足分别为点E、F.若OB=2,CF=6, .
.
(1)求点A的坐标;
(2)求一次函数和反比例函数的表达式.
某商店第一次用6000元购进了练习本若干本,第二次又用6000元购进该款练习本,但这次每本进货的价格是第一次进货价格的1.2倍,购进数量比第一次少了1000本.
(1)问:第一次每本的进货价是多少元?
(2)若要求这两次购进的练习本按同一价格全部销售完毕后获利不低于4500元,问每本售价至少是多少元?