若三个非零实数 , , 满足:只要其中一个数的倒数等于另外两个数的倒数的和,则称这三个实数 , , 构成“和谐三组数”.
(1)实数1,2,3可以构成“和谐三组数”吗?请说明理由;
(2)若 , , 三点均在函数 为常数, 的图象上,且这三点的纵坐标 , , 构成“和谐三组数”,求实数 的值;
(3)若直线 与 轴交于点 , ,与抛物线 交于 , , , 两点.
①求证: , , 三点的横坐标 , , 构成“和谐三组数”;
②若 , ,求点 , 与原点 的距离 的取值范围.
某商场用2500元购进了A、B两种新型节能台灯共50盏,这两种台灯的进价,标价如下表所示:
(1)这两种台灯各购进多少盏?
(2)若A型台灯按标价的九折出售,B型台灯按标价的八折出售,那么这批台灯全部售完后,商场共获利多少元?
已知三角形的第一边长为3a+2b,第二边比第一边长a-b,第三边比第二边短2a,求这个三角形的周长.
已知: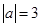 ,
, ,且
,且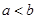 ,求
,求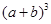 的值.
的值.
如果 ,那么
,那么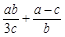 的值是多少?
的值是多少?
2008年6月1日起,我国实施“限塑令”,开始有偿使用环保购物袋.为了满足市场需求,某厂家生产A,B两种款式的布质环保购物袋,每天共生产4500个,两种购物袋的成本和售价如下表,设每天生产A种购物袋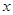 个,每天共获利
个,每天共获利 元.
元.
(1)求出 与
与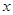 的函数关系式;
的函数关系式;
(2)如果该厂每天最多投入成本10000元,那么每天最多获利多少?