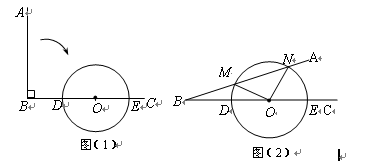
某次世界魔方大赛吸引世界各地共600名魔方爱好者参加,本次大赛首轮进行 阶魔方赛,组委会随机将爱好者平均分到20个区域,每个区域30名同时进行比赛,完成时间小于8秒的爱好者进入下一轮角逐;如图是 阶魔方赛 区域30名爱好者完成时间统计图,求:
① 区域 阶魔方爱好者进入下一轮角逐的人数的比例(结果用最简分数表示).
②若 阶魔方赛各个区域的情况大体一致,则根据 区域的统计结果估计在 阶魔方赛后进入下一轮角逐的人数.
③若 阶魔方赛 区域爱好者完成时间的平均值为8.8秒,求该项目赛该区域完成时间为8秒的爱好者的概率(结果用最简分数表示).

如图,在△ABC中,AB=AC,D是BC的中点,连结AD,在AD的延长线上取一点E,连结BE,CE.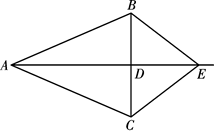
(1)求证:△ABE≌△ACE;
(2)当AE与AD满足什么数量关系时,四边形ABEC是菱形?并说明理由.
(1)计算:(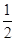 )-1-
)-1-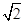 cos45°+3×(2012-π)0;(2)解不等式组:
cos45°+3×(2012-π)0;(2)解不等式组: ;
;
(3)化简: .
.
已知:矩形纸片ABCD中,AB=26厘米,BC=18.5厘米,点E在AD上,且AE=6厘米,点P是AB边上一动点.按如下操作:
步骤一,折叠纸片,使点P与点E重合,展开纸片得折痕MN(如图1所示);
步骤二,过点P作PT⊥AB,交MN所在的直线于点Q,连接QE(如图2所示)无论点P在AB边上任何位置,都有PQ_________QE(填“
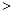 ”、“
”、“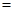 ”、“
”、“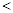 ”号);
”号);如图3所示,将纸片ABCD放在直角坐标系中,按上述步骤一、二进行操作:
①当点P在A点时,PT与MN交于点Q1,Q1点的坐标是(_______,_________);
②当PA=6厘米时,PT与MN交于点Q2. Q2点的坐标是(_______,_________);
③当PA=12厘米时,在图3中画出MN,PT(不要求写画法),并求出MN与PT的交点Q3的坐标;点P在运动过程,PT与MN形成一系列的交点Q1,Q2,Q3……观察、猜想:众多的交点形成的图象是什么?并直接写出该图象的函数表达式.
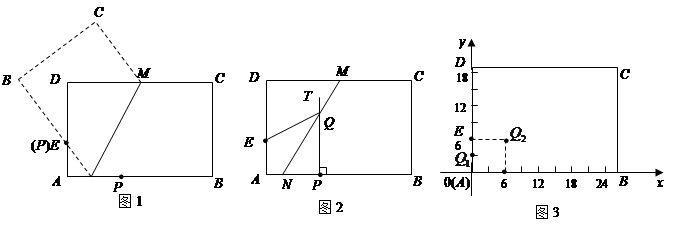
已知抛物线C1与x轴的一个交点为交于(-4,0),对称轴为直线x=-1.5,
并过点(-1,6)求抛物线C1的解析式;
求出与抛物线C1关于原点对称的抛物线C2的解析式,并在C1所在的平面直角坐标系中画出C2的图像;
在(2)的条件下,抛物线C1与抛物线C2与相交于A,B两点(点A在点B的左侧).
①求出点A和点B的坐标;
②点P在抛物线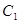 上,且位于点A和点B之间;点Q在抛物线
上,且位于点A和点B之间;点Q在抛物线 上,也位于点A和点B之间.当PQ∥
上,也位于点A和点B之间.当PQ∥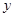 轴时,求PQ长度的最大值.
轴时,求PQ长度的最大值.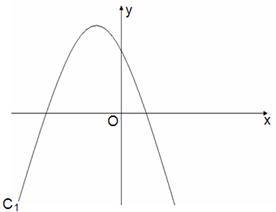
如图(1),∠ABC=90°,O为射线BC上一点,OB = 4,以点O为圆心, 长为半径作⊙O交BC于点D、E.
长为半径作⊙O交BC于点D、E.当射线BA绕点B按顺时针方向旋转多少度时与⊙O相切?请说明理由.
若射线BA绕点B按顺时针方向旋转600时与⊙O相交于M、N两点,如图(2),求的长。