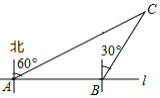
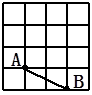如图,某市郊外景区内一条笔直的公路 经过 、 两个景点,景区管委会又开发了风景优美的景点 .经测量, 位于 的北偏东 的方向上, 位于 的北偏东 的方向上,且 .
(1)求景点 与 的距离;
(2)为了方便游客到景点 游玩,景区管委会准备由景点 向公路 修一条距离最短的公路,不考虑其他因素,求出这条最短公路的长.(结果保留根号)
为美化萧山,创建文明城市.园林部门决定利用现有的3600盆甲种花卉和2900盆乙种花卉搭配A、B两种园艺造型共50个,摆放在人民广场两侧,搭配每个造型所需花卉情况如下表所示:
| 造型 |
甲 |
乙 |
| A |
90盆 |
30盆 |
| B |
40盆 |
100盆 |
综合上述信息,解答下列问题:
(1)符合题意的搭配方案有哪几种?
(2)若搭配一个A型造型的成本为1000元,
搭配一个B型造型的成本为1200元.试说明运用(1)中哪种方案成本最低?
我市体校准备挑选一名跳高运动员参加全市中学生运动会,对跳高运动队的甲、乙两名运动员进行了8次选拔比赛,他们的成绩(单位:cm)如下:
甲:170 165 168 169 172 173 168 167
乙:160 173 172 161 162 171 170 175
(1)甲、乙两名运动员的跳高平均成绩分别是多少?
(2)哪名运动员的成绩更为稳定?为什么?
(3)若预测,跳过165cm就很可能获得冠军。该校为了获得冠军,可能选哪位运动员参赛?若预测跳过170cm才能得冠军呢?
在平面直角坐标系中, △ABC的三个顶点的位置如图所示,点A'的坐标是
(-2,2), 现将△ABC平移,使点A变换为点A',点B′、C′分别是B、C的对应点。
(1)请画出平移后的像△A'B'C'(不写画法) ,并直接写出点B′、C′的坐标:
B′ () 、C′ () ;
(2)若△ABC 内部一点P的坐标为(a,b),则点P 的对应点P ′的坐标是 () .
如图,CD=BE,DG⊥BC,EF⊥BC,垂足分别为G,F,且DG=EF。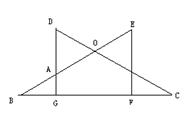
(1)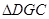 与
与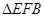 全等吗?请说明理由;
全等吗?请说明理由;
(2)OB=OC吗?请说明理由;
(3)若∠B=30°,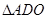 的形状是
的形状是
请在下图方格中任画出两个以AB腰的等腰三角形ABC。(要求:一个为锐角三角形,一个为钝角三角形)