如图1，在矩形ABCD中，E是AD的中点，以点E为直角顶点的-优题课

游客

题文

如图1，在矩形 $ABCD$ 中， $E$ 是 $AD$ 的中点，以点 $E$ 为直角顶点的直角三角形 $EFG$ 的两边 $EF$ ， $EG$ 分别过点 $B$ ， $C$ ， $∠ F = 30 °$ ．

（1）求证： $BE = CE$ ；

（2）将 $ΔEFG$ 绕点 $E$ 按顺时针方向旋转，当旋转到 $EF$ 与 $AD$ 重合时停止转动，若 $EF$ ， $EG$ 分别与 $AB$ ， $BC$ 相交于点 $M$ ， $N$ （如图 $2)$ ．

①求证： $ΔBEM ≅ ΔCEN$ ；

②若 $AB = 2$ ，求 $ΔBMN$ 面积的最大值；

③当旋转停止时，点 $B$ 恰好在 $FG$ 上（如图 $3)$ ，求 $\sin ∠ EBG$ 的值．

科目数学题型解答题难度中等

知识点：旋转的性质矩形的性质全等三角形的判定与性质二次函数的应用四边形综合题等腰直角三角形

登录免费查看答案和解析

相关试题

解方程
（1）
（2）

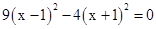
如图，已知在矩形ABCD中，AB＝2，BC＝3，P是线段AD边上的任意一点（不含端点A、D），连结PC，过点P作PE⊥PC交AB于E．

（1）证明△PAE∽△CDP；
（2）当点P在AD上运动时，对应的点E也随之在AB上运动，设AP＝x，BE＝y，求y与x的函数关系式及y的取值范围；
（3）在线段AD上是否存在不同于P的点Q，使得QC⊥QE？若存在，求线段AP与AQ之间的数量关系；若不存在，请说明理由．

如图，P₁是反比例函数在第一象限图象上的一点，已知△P₁O A₁为等边三角形，点A₁的坐标为(2，0)．

（1）直接写出点P₁的坐标；
（2）求此反比例函数的解析式；
（3）若△P₂A₁A₂为等边三角形，求点A₂的坐标．

某市为落实房地产调控政策，加快了廉租房的建设力度．第一年投资2亿元人民币建设了廉租房8万平方米，累计连续三年共投资9.5亿元人民币建设廉租房.设每年投资的增长率均为．
(1)求每年投资的增长率；
(2)若每年建设成本不变，求第三年建设了多少万平方米廉租房．

如图，在平面直角坐标系中，△ABC和△是以坐标原点O为位似中心的位似图形，且点B（3，1），B′（6，2）.

（1）请你根据位似的特征并结合点B的坐标变化回答下列问题： ①若点A（，3），则A′的坐标为；②△ABC与△的相似比为；
（2）若△ABC的面积为m，求△A′B′C′的面积.（用含m的代数式表示）

试卷网试题网古诗词网作文网范文网