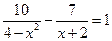已知抛物线 的图象经过坐标原点 ,且与 轴另一交点为 , .

(1) 求抛物线 的解析式;
(2) 如图 1 ,直线 与抛物线 相交于点 , 和点 , (点 在第二象限) ,求 的值 (用 含 的式子表示) ;
(3) 在 (2) 中, 若 ,设点 是点 关于原点 的对称点, 如图 2 .
①判断△ 的形状, 并说明理由;
②平面内是否存在点 ,使得以点 、 、 、 为顶点的四边形是菱形?若存在, 求出点 的坐标;若不存在, 请说明理由 .
(本题8分) 已知二次函数 的图象与
的图象与 轴两交点的坐标分别为(
轴两交点的坐标分别为( ,0),(
,0),( ,0)(
,0)( ).
).
(1)证明 ;
;
(2)若该函数图象的对称轴为直线 ,试求二次函数的最小值.
,试求二次函数的最小值.
(本题8分) 在国家的宏观调控下,某市的商品房成交价由今年7月份的14000元/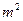 下降到9月份的12600元/
下降到9月份的12600元/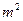
⑴求8、9两月平均每月降价的百分率是多少?(参考数据: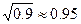 )
)
⑵如果房价继续回落,按此降价的百分率,你预测到11月份该市的商品房成交均价是否会跌破10000元/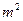 ?请说明理由。
?请说明理由。
(本题8分)
已知:抛物线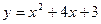 与x轴相交于A、B两点(A点在B点的左侧),顶点为P.
与x轴相交于A、B两点(A点在B点的左侧),顶点为P.
(1)求A、B、P三点坐标;
(2)画出此抛物线的简图,并根据简图直接写出当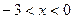 时,函数值y的取值范围
时,函数值y的取值范围
(本题8分)关于x的一元二次方程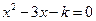 有两个不相等的实数根.
有两个不相等的实数根.
(1)求k的取值范围.
(2)请选择一个k的负整数值,并求出方程的根.
(每小题6分,共18分)解下列方程:
①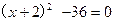
②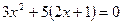
③