某公司设计了一款产品，每件成本是50元，在试销期间，据市场调查，销售单价是60元时，每天的销量是250件，而销售单价每增加1元，每天会少售出5件，公司决定销售单价 （元 不低于60元，而市场要求 不得超过100元．
（1）求出每天的销售量 （件 与销售单价 （元 之间的函数关系式，并写出 的取值范围；
（2）求出每天的销售利润 （元 与销售单价 （元 之间的函数关系式，并求出当 为多少时，每天的销售利润最大，并求出最大值；
（3）若该公司要求每天的销售利润不低于4000元，但每天的总成本不超过6250元，则销售单价 最低可定为多少元？
求值：（2+1）•（22+1）•（24+1）•（28+1）•（216+1）﹣232．
利用平方差公式计算99992．
利用图形来表示数量或数量关系，也可以利用数量或数量关系来描述图形特征或图形之间的关系，这种思想方法称为数形结合．我们刚学过的《从面积到乘法公式》就很好地体现了这一思想方法，你能利用数形结合的思想解决下列问题吗？
如图，一个边长为1的正方形，依次取正方形的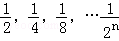
，根据图示我们可以知道：第一次取走
后还剩，即=1﹣；前两次取走+
后还剩，即+
=1﹣；前三次取走
++
后还剩，即++=1﹣；…前n次取走后，还剩 _________ ，即 _________ = _________ ．
利用上述计算：
（1）
= _________ ．
（2）
= _________ ．
（3）2﹣22﹣23﹣24﹣25﹣26﹣…﹣22011+22012（本题写出解题过程）
“*”是规定的一种运算法则：a*b=a2﹣b．
①求5*（﹣1）的值；
②若3*x=2，求x的值；
③若（﹣4）*x=2+x，求x的值．
大家已经知道，完全平方公式和平方差公式可以用平面几何图形的面积来表示，实际上还有一些代数恒等式也可以用这种形式表示，例如：2x（x+y）=2x2+2xy就可以用图的面积表示．
（1）请写出图（2）所表示的代数恒等式： _______ ；
（2）请写出图（3）所表示的代数恒等式： ________ ；
（3）试画出一个几何图形，使它的面积能表示（x+y）（x+3y）=x2+4xy+3y2．