阅读下面材料：
小明遇到这样一个问题：
如图1， 中， ，点 在 上，且 ，求证： ．
小明发现，除了直接用角度计算的方法外，还可以用下面两种方法：
方法1：如图2，作 平分 ，与 相交于点 ．
方法2：如图3，作 ，与 相交于点 ．
（1）根据阅读材料，任选一种方法，证明 ．
用学过的知识或参考小明的方法，解决下面的问题：
（2）如图4， 中，点 在 上，点 在 上，且 ，点 在 上，且 ，延长 、 ，相交于点 ，且 ．
①在图中找出与 相等的角，并加以证明；
②若 ，猜想线段 与 的数量关系，并证明你的猜想．
如图1，矩形MNPQ中，点E，F，G，H分别在NP，PQ，QM，MN上，若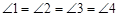
，则称四边形EFGH为矩形MNPQ的反射四边形．图2，图3，图4中，四边形ABCD为矩形，且
，
．
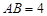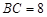理解与作图：
（1）在图2，图3中，点E，F分别在BC，CD边上，试利用正方形网格在图上作出矩形ABCD的反射四边形EFGH．
计算与猜想：
（2）求图2，图3中反射四边形EFGH的周长，并猜想矩形ABCD的反射四边形的周长是否为定值？
启发与证明：
（3）如图4，为了证明上述猜想，小华同学尝试延长GF交BC的延长线于M，试利用小华同学给我们的启发证明（2）中的猜想．
某景区的旅游线路如图1所示，其中A为入口，B，C，D为风景点，E为三岔路的交汇点，图1中所给数据为相应两点间的路程（单位：km）．甲游客以一定的速度沿线路“A→D→C→E→A”步行游览，在每个景点逗留的时间相同，当他回到A处时，共用去3h．甲步行的路程s（km）与游览时间t（h）之间的部分函数图象如图2所示．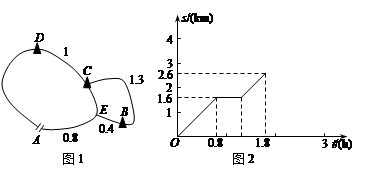
（1）求甲在每个景点逗留的时间，并补全图象；
（2）求C，E两点间的路程；
（3）乙游客与甲同时从A处出发，打算游完三个景点后回到A处，两人相约先到者在A处等候， 等候时间不超过10分钟．如果乙的步行速度为3km/h，在每个景点逗留的时间与甲相同，他们的约定能否实现？请说明理由．
如图，AB是⊙O的直径，点E是AB上的一点，CD是过E点的弦，过点B的切线交AC的延长线于点F，BF∥CD，连接BC．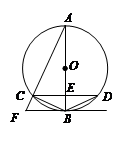
（1）已知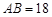
，
，求弦CD的长；
（2）连接BD，如果四边形BDCF为平行四边形，则点E位于AB的什么位置？试说明理由．
某校举行以“助人为乐，乐在其中”为主题的演讲比赛，比赛设一个第一名，一个第二名，两个并列第三名．前四名中七、八年级各有一名同学，九年级有两名同学，小蒙同学认为前两名是九年级同学的概率是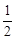
，你赞成他的观点吗？请用列表法或画树形图法分析说明．
如图，一次函数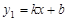
的图象与反比例函数
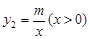的图象交于A（1，6），B（
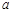，2）两点．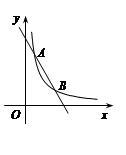
（1）求一次函数与反比例函数的解析式；
（2）直接写出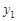
≥
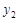时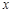
的取值范围．