某景区的旅游线路如图1所示,其中A为入口,B,C,D为风景点,E为三岔路的交汇点,图1中所给数据为相应两点间的路程(单位:km).甲游客以一定的速度沿线路“A→D→C→E→A”步行游览,在每个景点逗留的时间相同,当他回到A处时,共用去3h.甲步行的路程s(km)与游览时间t(h)之间的部分函数图象如图2所示.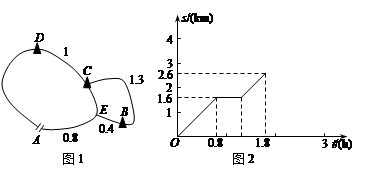
(1)求甲在每个景点逗留的时间,并补全图象;
(2)求C,E两点间的路程;
(3)乙游客与甲同时从A处出发,打算游完三个景点后回到A处,两人相约先到者在A处等候, 等候时间不超过10分钟.如果乙的步行速度为3km/h,在每个景点逗留的时间与甲相同,他们的约定能否实现?请说明理由.
有一块直角三角板XYZ放置在△ABC上,三角板XYZ的两条直角边XY、XZ恰好分别经过点B、C。△ABC中,
(1)如图1,若∠A=30°.则∠ABC+∠ACB=度,∠XBC+∠XCB=度;
(2)如图2,改变直角三角板XYZ的位置,使三角板XYZ的两条直角边XY、XZ仍然分别经过点B、C,若∠A=x°,则∠ABX+∠ACX=度;(用x的代数式表示)
今年清明节,小明和爸爸决定用游戏的方式确定两个城市作为旅游目的地。他们把3张分别写着“上海”、“杭州”、“宁波”的卡片放入不透明的A口袋,把2张分别写着“苏州”、“南京”的卡片放入不透明的B口袋。小明从A口袋中随机抽取一张卡片,爸爸从B口袋中随机抽取一张卡片,以抽到的两张卡片上写着的城市为旅游目的地。
(1)请你用列树状图或列表法来说明,他们共有多少种旅游方案?
(2)恰好抽到小明最喜欢去的两个城市——“杭州”和“苏州”的概率是多少?
如图,在正方形格上有一个△DEF。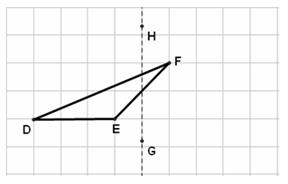
(1)作△DEF关于直线HG的轴对称图形(不写作法);
(2)作EF边上的高(不写作法);
(3)若格上的最小正方形边长为1,求△DEF的面积为__________。
在下面过程中的横线上填空,并在括号内注明理由。
如图,已知∠B =∠C,AD = AE,说明DB与EC相等。
解: 在△ABE和△ACD中
∠B = _______(已知)
_______ = _______()
AD =" AE" (已知)
∴△ABE ≌△ACD ()
∴AB = AC()
又∵AD = AE
∴ AB-AD=AC-AE,
即 DB = EC.
解方程组: