（本题10分） 烟台享有“苹果之乡”的美誉．甲、乙两超市分别用3000元以相同的进价购进质量相同的苹果．甲超市销售方案是：将苹果按大小分类包装销售，其中大苹果400千克，以进价的2倍价格销售，剩下的小苹果以高于进价10%销售．乙超市的销售方案是：不将苹果按大小分类，直接包装销售，价格按甲超市大、小两种苹果售价的平均数定价．若两超市将苹果全部售完，其中甲超市获利2100元（其它成本不计）．问：（1）苹果进价为每千克多少元？
（2）乙超市获利多少元？并比较哪种销售方式更合算．
（本小题满分5分）
已知直线
经过点M（2，1），且与x轴交于点A，与y轴交于点B．
（1）求k的值；
（2）求A、B两点的坐标；
（3）过点M作直线MP与y轴交于点P，且△MPB的面积为2，求点P的坐标．
（本小题满分5分）
在△ABC中，AC=BC，∠ACB=90°，AB=6，过点C作射线CP∥AB，在射线CP上截取CD=2，联结AD，求AD的长．
（本小题满分5分）列方程或方程组解应用题：
某学校组织九年级学生参加社会实践活动，若单独租用35座客车若干辆，则刚好坐满；若单独租用55座客车，则可以少租一辆，且余45个空座位，求该校九年级学生参加社会实践活动的人数．
本小题满分5分）
已知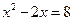
，求代数式
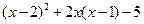的值．
（本小题满分5分）
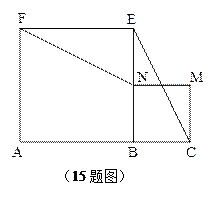
如图，A、B、C三点在同一条直线上，AB=2BC，分别以AB，BC为边做正方形ABEF和正方形BCMN，联结FN，EC． 求证：FN=EC