如图,在 中, , , 于点 .
(1)如图1,点 , 在 , 上,且 .求证: ;
(2)点 , 分别在直线 , 上,且 .
①如图2,当点 在 的延长线上时,求证: ;
②当点 在点 , 之间,且 时,已知 ,直接写出线段 的长.

如图,在边长为1的小正方形组成的网格中, 的三个顶点均在格点上,点A、B的坐标分别为
的三个顶点均在格点上,点A、B的坐标分别为

(1)画出 绕点O顺时针旋转
绕点O顺时针旋转 后的
后的 ;
;
(2)写出点 的坐标;
的坐标;
(3)求四边形 的面积.
的面积.
关于 的方程为
的方程为 .
.
(1)证明:方程有两个不相等的实数根.
(2)是否存在实数m,使方程的两个实数根互为相反数?若存在,求出m的值及两个实数根;若不存在,请说明理由
一道选择题共有A、B、C、D四个备选答案,
(1)如果其中只有一个是正确的,某位同学随意选了其中一个答案,他选中正确答案的概率是多少?
(2)如果其中有两个是正确的,某位同学随意选了其中两个答案,他选中正确答案的概率是多少?
如图,将一把两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心 ,另一边所在直线与半圆相交于点
,另一边所在直线与半圆相交于点 ,量出半径
,量出半径 ,弦
,弦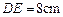 ,求直尺的宽度.
,求直尺的宽度.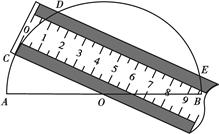
解方程组