某学校开展“科技创新大赛”活动,设计遥控车沿直线轨道做匀速直线运动
的模型.现在甲、乙两车同时分别从不同起点A,B出发,沿同一轨道到达C处.设t后甲、乙两遥控车与B处的距离分别为d1,d2,且d1,d2与t的函数关系如图,若甲的速度是乙的速度的1.5倍,试根据图象解决下列问题: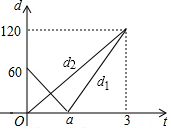
(1)填空:乙的速度是米/分;
(2)写出d1与t的函数关系式;
(3)若甲、乙两遥控车的距离超过10米时信号不会产生相互干扰,试探求什么时间两遥控车的信号不会产生相互干扰?
某公司招聘人才,共有50人进入复试.对应聘者分别进行阅读能力、思维能力和表达能力三项侧试,甲、乙两人的成绩如表(单位:分):
| 阅读 |
思维 |
表达 |
|
| 甲 |
93 |
86 |
73 |
| 乙 |
95 |
81 |
79 |
(1)根据实际需要,公司将阅读、思维和表达能力三项测试得分按3:5:2确定每人的最后成绩,若按此成绩在甲、乙两人中录用一人,谁将被录用?
(2)公司按照(1)中的成绩计算方法,将每位应聘者的最后成绩绘制成如图所示的频数分布直方图,请计算此次参加复试人员的平均分.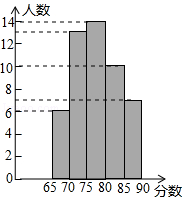
如图,四边形ABCD是矩形,∠EDC=∠CAB,∠DEC=90°.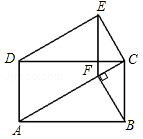
(1)求证:AC∥DE;
(2)过点B作BF⊥AC于点F,连接EF,试判别四边形BCEF的形状,并说明理由.
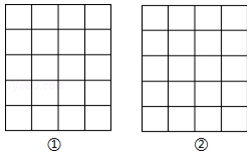
如图,正方形网格中,每个小正方形的边长均为1,每个小正方形的顶点叫格点,以格点为顶点按下列要求画图:
(1)在图①中画一条线段MN,使MN=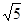 ;
;
(2)在图②中画一个△ABC,使其三边长分别为3,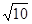 ,
,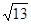 .
.
探究题:如图:
(1)△ABC为等边三角形,动点D在边CA上,动点P在边BC上,若这两点分别从C、B点同时出发,以相同的速度由C向A和由B向C运动,连接AP,BD交于点Q,两点运动过程中AP=BD成立吗?请证明你的结论;
(2)如果把原题中“动点D在边CA上,动点P边BC上,”改为“动点D,P在射线CA和射线BC上运动”,其他条
件不变,如图(2)所示,两点运动过程中∠BQP的大小保持不变.请你利用图(2)的情形,
求证:∠BQP=60°;
(3)如果把原题中“动点P在边BC上”改为“动点P在AB的延长线上运动,连接PD交BC于E”,其他条件不变,如图(3),则动点D,P在运动过程中,DE始终等于PE吗?写出证明过程.