为迎接“七 一”党的生日，某校准备组织师生共310人参加一次大型公益活动，租用4辆大客车和6辆小客车恰好全部坐满，已知每辆大客车的座位数比小客车多15个．
（1）求每辆大客车和每辆小客车的座位数；
（2）经学校统计，实际参加活动的人数增加了40人，学校决定调整租车方案，在保持租用车辆总数不变的情况下，为使所有参加活动的师生均有座位，最多租用小客车多少辆？
请用直尺和圆规在所给的两个矩形中各作一个不为正方形的菱形，且菱形的四个顶点都在矩形的边上，面积相同的图形视为同一种.(保留作图痕迹).
如图，已知直线
过点
和
，
是
轴正半轴上的动点，
的垂直平分线交于点
，交轴于点
．
（1）直接写出直线的解析式；
（2）当
时，设
，
的面积为
，求S关于t的函数关系式；并求出S的最大值；
（3）当点Q在线段AB上（Q与A、B不重合）时，直线
过点A且与x轴平行，问在上是否存在点C，使得
是以为直角顶点的等腰直角三角形？若存在，求出点C的坐标，并证明；若不存在，请说明理由．
北京奥运会开幕前，某体育用品商场预测某品牌运动服能够畅销，就用32000元购进了一批这种运动服，上市后很快脱销．商场又用68000元购进第二批这种运动服，所够数量是第一批购进数量的2倍，但每套进价多了10元．
（1）该商场两次共购进这种牌运动服多少套？
（2）如果这两批运动服每套的售价相同，且全部售完后总利润率不低于20%，那么每套售价至少是多少元？（
）
已知：如图，⊙O是△ABC的外接圆，AB为⊙O直径，且PA⊥AB于点Ａ，PO⊥AC于点M．
（1）求证：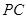
是⊙
的切线；
（2）当
，
时，求PC的长．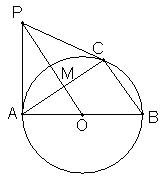
如图，在□ABCD中，E、F分别是AB、CD的中点，连接AF、CE．
（1）求证：△BEC≌△DFA；
（2）连接AC，当CA＝CB时，判断四边形AECF是什么特殊四边形？并证明你的结论．