如图，ΔABC与ΔCDE是等边三角形，连接AD，取AD的中点-优题课

题文

如图， $ΔABC$ 与 $ΔCDE$ 是等边三角形，连接 $AD$ ，取 $AD$ 的中点 $P$ ，连接 $BP$ 并延长至点 $M$ ，使 $PM = BP$ ，连接 $AM$ ， $EM$ ， $AE$ ，将 $ΔCDE$ 绕点 $C$ 顺时针旋转．

（1）如图1，当点 $D$ 在 $BC$ 上，点 $E$ 在 $AC$ 上时，则 $ΔAEM$ 的形状为　　；

（2）将 $ΔCDE$ 绕点 $C$ 顺时针旋转至图2的位置，请判断 $ΔAEM$ 的形状，并说明理由；

（3）若 $CD = \frac{1}{2} BC$ ，将 $ΔCDE$ 由图1位置绕点 $C$ 顺时针旋转 $α (0 ° ⩽ α < 360 °)$ ，当 $ME = \sqrt{3} CD$ 时，请直接写出 $α$ 的值．

科目数学题型解答题难度中等

知识点：旋转的性质几何变换综合题等边三角形的判定与性质

登录免费查看答案和解析

相关试题

某海滨浴场东西走向的海岸线可以近似看作直线l(如图).救生员甲在A处的瞭望台上观察海面情况，发现其正北方向的B处有人发出求救信号，他立即沿AB方向径直前往救援，同时通知正在海岸线上巡逻的救生员乙.乙马上从C处入海,径直向B处游去.甲在乙入海10秒后赶到海岸线上的D处,再向B处游去.若CD=40米,B在C的北偏东35°方向,甲乙的游泳速度都是2米/秒.问谁先到达B处？请说明理由.
(参考数据：sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)

一个不透明的袋中装有红、黄、白三种颜色的球共100个,它们除颜色外都相同，其中黄球的个数是白球个数的2倍少5个，已知从袋中摸出一个球是红球的概率是.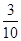
求袋中红球的个数；
求从袋中摸出一个球是白球的概率；
取走10个球(其中没有红球)后,求从剩余的球中摸出一个球是红球的概率.

如图，△ABC中，∠B=90°，AB=6cm，BC=8cm，将△ABC沿射线BC方向平移10cm，得到△DEF，A，B，C的对应点分别是D,E,F，连结AD，求证：四边形ACFD是菱形。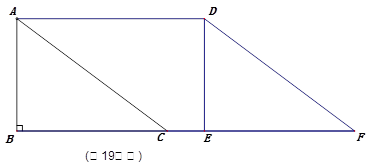

如图，在方格纸中，△PQR的三个顶点及A,B,C,D,E五个点都在小方格的顶点上，现以A,B,C,D,E中的三个顶点为顶点画三角形，

在图甲中画出一个三角形与△PQR全等
在图乙中画出一个三角形与△PQR面积相等但不全等

解方程：x²－2x=5

试卷网试题网古诗词网作文网范文网