在创建“文明校园”活动中，某校有2名男生和3名女生被评为学校“文明学生”．现要从这5名学生中选拔“学校文明礼仪值周岗”的值周生．
（1）从这5名学生中随机选拔1人值周，恰好选到男生的概率是 ．
（2）从这5名学生中随机选拔2人值周，请用树状图或列表法求出恰好选到1个男生和1个女生的概率．
如图，直线AB分别交y轴、x 轴于A、B两点，OA=2，
，抛物线
过A、B两点.
（1）求直线AB和这个抛物线的解析式；
（2）设抛物线的顶点为D，求△ABD的面积
（3）作垂直x轴的直线x=t，在第一象限交直线AB于M，交这个抛物线于N.求当t 取何值时，MN的长度l有最大值？最大值是多少？
如图，梯形ABCD中，AD//BC，E为CD边的中点，F为AD延长线上一点，且满足DF+BF=BC.
（1）若∠A=90º，AD=3，AB=5，BC=9，求BE的长；
（2）求证：BE平分∠FBC.
为奖励“我的中国梦”暑期系列实践活动的获奖学生，学校准备在某商店购买A，B两种文具作为奖品，已知一件A种文具的单价比B种文具的单价便宜4元，而用300元买A种文具的件数是用200元买B种文具的件数的2倍．
（1）求A种文具的单价；
（2）根据需要，学校准备在该商店购买A，B两种文具共200件，其中A种文具的件数不多于B种文具件数的3倍．为了节约经费，应购买A，B两种文具各多少件？使用经费最少为多少元？
已知抛物线y＝ax2＋bx＋c经过A(－1，0)、B(3，0)、C(0，3)三点，直线l是抛物线的对称轴．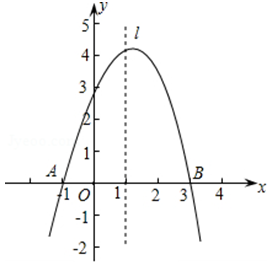
(1)求抛物线的函数关系式；
(2)设点P是直线l上的一个动点，当△PAC的周长最小时，求点P的坐标，并求出此时的周长；
(3)在直线l上是否存在点M，使△MAC为直角三角形？若存在，请写出所有符合条件的点M的坐标；若不存在，请说明理由．
锐角△ABC中，BC=6，
，两动点M,N分别在边AB,AC上滑动，且MN∥BC，以MN为边向下作正方形MPQN，设其边长为x，正方形MPQN与△ABC公共部分的面积为y(y＞0)．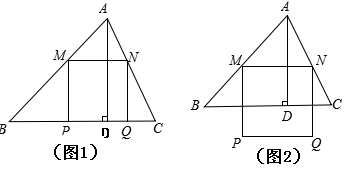
(1)求△ABC中边BC上高AD；
(2)当x为何值时，PQ恰好落在边BC上（如图1）；
(3)当PQ在△ABC外部时（如图2），求y关于x的函数关系式（注明x的取值范围），并求出x为何值时y最大，最大值是多少？