如图,在平面直角坐标系中,一次函数 的图象与 轴交于点 ,与反比例函数 的图象交于 , 两点,点 在第一象限,纵坐标为4,点 在第三象限, 轴,垂足为点 , .
(1)求反比例函数和一次函数的解析式.
(2)连接 , ,求四边形 的面积.

已知:如图,点B、C、E在同一条直线上,AC∥DE,AC=CE,BC=DE,求证:AB=CD。
分解因式:(1)n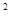 (m-2)-n(2-m);(2)2a
(m-2)-n(2-m);(2)2a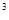 -4a
-4a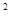 b+2ab
b+2ab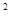 ;
;
先化简再求值:4(m+1)2-(2m+5)(2m-5),其中m=-3。
计算:(1)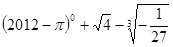 ;(2)(2a)3b4÷12a3b2
;(2)(2a)3b4÷12a3b2
如图,在直角坐标系中,⊙P与y轴相切于点C,与x轴交于A(x1,0),B(x2,0)两点,其中x1,x2是方程x2-10x+16=0的两个根,且x1<x2,连接BC,AC.
(1)求过A、B、C三点的抛物线的解析式;
(2)在抛物线的对称轴上是否存在点Q,使△QAC的周长最小,若存在求出点Q的坐标,若不存在,请说明理由;
(3)点M在第一象限的抛物线上,当△MBC的面积最大时,求点M的坐标.