分解因式:(1)n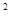 (m-2)-n(2-m);(2)2a
(m-2)-n(2-m);(2)2a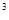 -4a
-4a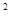 b+2ab
b+2ab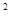 ;
;
根据给出的下列两种情况,请用直尺和圆规找到一条直线,把△ABC恰好分割成两个等腰三角形(不写做法,但需保留作图痕迹);并根据每种情况分别猜想:∠A与∠B有怎样的数量关系时才能完成以上作图?并举例验证猜想所得结论.
(1)如图①△ABC中,∠C=90°,∠A=24°
①作图:
②猜想:
③验证:
(2)如图②△ABC中,∠C=84°,∠A=24°.
①作图:
②猜想:
③验证:
如图,直线PM切⊙O于点M,直线PO交⊙O于A、B两点,弦AC∥PM,连接OM、BC.
求证:(1)△ABC∽△POM;(2)2OA2=OP•BC.
甲、乙两名同学进行射击训练,在相同条件下各射靶5次,成绩统计如下:
| 命中环数 |
7 |
8 |
9 |
10 |
| 甲命中相应环数的次数 |
2 |
2 |
0 |
1 |
| 乙命中相应环数的次数 |
1 |
3 |
1 |
0 |
若从甲、乙两人射击成绩方差的角度评价两人的射击水平,则谁的射击成绩更稳定些?
依据下列解方程 的过程,请在前面的括号内填写变形步骤,在后面的括号内填写变形依据.
的过程,请在前面的括号内填写变形步骤,在后面的括号内填写变形依据.
解:原方程可变形为 ( )
( )
去分母,得3(3x+5)=2(2x﹣1).( )
去括号,得9x+15=4x﹣2. ( )
( )
( ),得9x﹣4x=﹣15﹣2.( )
合并,得5x=﹣17.( )
( ),得x= .( )
.( )
在平面直角坐标系中,抛物线y=ax2+bx+3与x轴的两个交点分别为A(﹣3,0)、B(1, 0),过顶点C作CH⊥x轴于点H.
0),过顶点C作CH⊥x轴于点H.
(1)直接填写:a= ,b= ,顶点C的坐标为 ;
(2 )在y轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
)在y轴上是否存在点D,使得△ACD是以AC为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
(3)若点P为x轴上方的抛物线上一动点(点P与顶点C不重合),PQ⊥AC于点Q,当△PCQ与△ACH相似时,求点P的坐标.