把函数 的图象绕点 旋转 ,得到新函数 的图象,我们称 是 关于点 的相关函数. 的图象的对称轴与 轴交点坐标为 .
(1)填空: 的值为 (用含 的代数式表示)
(2)若 ,当 时,函数 的最大值为 ,最小值为 ,且 ,求 的解析式;
(3)当 时, 的图象与 轴相交于 , 两点(点 在点 的右侧).与 轴相交于点 .把线段 原点 逆时针旋转 ,得到它的对应线段 ,若线 与 的图象有公共点,结合函数图象,求 的取值范围.
(本题12分)正方形ABCD和正方形AEFG有公共顶点A,将正方形AEFG绕点A按顺时针方向旋转,记旋转角∠DAG=α,其中0°≤α≤180°,连结DF,BF,如图。
(1)若α=0°,则DF=BF,请加以证明;
(2)试画一个图形(即反例),说明(1)中命题的逆命题是假命题;
(3)对于(1)中命题的逆命题,如果能补充一个条件后能使该逆命题为真命题,请直接写出你认为需要补充的一个条件,不必说明理由。
(本题12分)某校规划在一块长AD为18m,宽AB为13m的长方形场地ABCD上,设计分别与AD,AB平行的横向通道和纵向通道,其余部分铺上草皮。
(1)如图1,若设计三条通道,一条横向,两条纵向,且它们的宽度相等,其余六块草坪相同,其中一块草坪两边之比AM:AN=8:9,问通道的宽是多少?
(2)为了建造花坛,要修改(1)中的方案,如图2,将三条通道改为两条通道,纵向的宽度改为横向宽度的2倍,其余四块草坪相同,且每一块草坪均有一边长为8m,这样能在这些草坪建造花坛。如图3,在草坪RPCQ中,已知RE⊥PQ于点E,CF⊥PQ于点F,求花坛RECF的面积。
(本题10分)如果抛物线 过定点M(1,1),则称此抛物线为定点抛物线。
过定点M(1,1),则称此抛物线为定点抛物线。
(1)张老师在投影屏幕上出示了一个题目:请你写出一条定点抛物线的一个解析式。小敏写出了一个答案: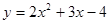 ,请你写出一个不同于小敏的答案;
,请你写出一个不同于小敏的答案;
(2)张老师又在投影屏幕上出示了一个思考题:已知定点抛物线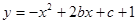 ,求该抛物线顶点纵坐标的值最小时的解析式,请你解答。
,求该抛物线顶点纵坐标的值最小时的解析式,请你解答。
(本题8分)如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走6m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°。
(1)求∠BPQ的度数;
(2)求该电线杆PQ的高度(结果精确到1m)。备用数据: ,
,
(本题8分)为了解某种电动汽车的性能,对这种电动汽车进行了抽检,将一次充电后行驶的里程数分为A,B,C,D四个等级,其中相应等级的里程依次为200千米,210千米,220千米,230千米,获得如下不完整的统计图。
根据以上信息,解答下列问题:
(1)问这次被抽检的电动汽车共有几辆?并补全条形统计图;
(2)估计这种电动汽车一次充电后行驶的平均里程数为多少千米?