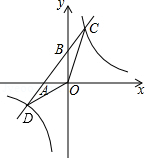
如图,一次函数 的图象与 轴、 轴分别交于 , 两点,与反比例函数 的图象分别交于 , 两点,点 ,点 是线段 的中点.
(1)求一次函数 与反比例函数 的解析式;
(2)求 的面积;
(3)直接写出当 取什么值时, .
如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,过点C作CF∥BE交DE的延长线于F.
(1)求证:四边形BCFE是菱形;
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
如图,把圆形转盘A平均4等份、圆形转盘B平均3等份,并在每一个小区域内标上数字.欢欢、乐乐两个人玩转盘游戏,游戏规则如下:同时转动两个转盘,当转盘停止时,若指针所指两区域的数字之积为奇数,则欢欢胜;若指针所指两区域的数字之积为偶数,则乐乐胜;若有指针落在分割线上,则无效,重转.
(1)若单独自由转动A盘,当它停止转动时,指针指向奇数区的概率是 .
(2)用列表或画树状图的方法求出欢欢获胜的概率.
解方程:2x2-9x+8=0.
已知:如图,菱形ABCD中,对角线AC,BD相交于点O,且AC=12cm,BD=16cm.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,直线EF从点D出发,沿DB方向匀速运动,速度为1cm/s,EF⊥BD,且与AD,BD,CD分别交于点E,Q,F;当直线EF停止运动时,点P也停止运动.连接PF,设运动时间为t(s)(0<t<8).解答下列问题: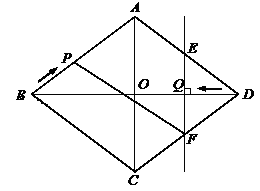
(1)当t为何值时,四边形APFD是平行四边形?
(2)设四边形APFE的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使S四边形APFE:S菱形ABCD=17:40?若存在,求出t的值,并求出此时P,E两点间的距离;若不存在,请说明理由.
如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求证:CE=AD;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.