已知:如图,菱形ABCD中,对角线AC,BD相交于点O,且AC=12cm,BD=16cm.点P从点B出发,沿BA方向匀速运动,速度为1cm/s;同时,直线EF从点D出发,沿DB方向匀速运动,速度为1cm/s,EF⊥BD,且与AD,BD,CD分别交于点E,Q,F;当直线EF停止运动时,点P也停止运动.连接PF,设运动时间为t(s)(0<t<8).解答下列问题: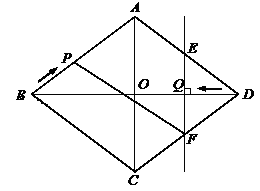
(1)当t为何值时,四边形APFD是平行四边形?
(2)设四边形APFE的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使S四边形APFE:S菱形ABCD=17:40?若存在,求出t的值,并求出此时P,E两点间的距离;若不存在,请说明理由.
如图,P为正方形ABCD的边BC上一动点(P与B、C不重合),连接AP,过点B作BQ⊥AP交CD于点Q,将△BQC沿BQ所在的直线对折得到△BQC′,延长QC′交BA的延长线于点M.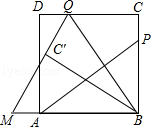
(1)试探究AP与BQ的数量关系,并证明你的结论;
(2)当AB=3,BP=2PC,求QM的长;
(3)当BP=m,PC=n时,求AM的长.
如图,在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A,交AB于点D,交CA的延长线于点E,过点E作AB的平行线EF交⊙A于点F,连接AF,BF,DF.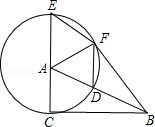
(1)求证:△ABC≌△ABF;
(2)当∠CAB等于多少度时,四边形ADFE为菱形?请给予证明.
假如娄底市的出租车是这样收费的:起步价所包含的路程为0~1.5千米,超过1.5千米的部分按每千米另收费.
小刘说:“我乘出租车从市政府到娄底汽车站走了4.5千米,付车费10.5元.”
小李说:“我乘出租车从市政府到娄底汽车站走了6.5千米,付车费14.5元.”
问:(1)出租车的起步价是多少元?超过1.5千米后每千米收费多少元?
(2)小张乘出租车从市政府到娄底南站(高铁站)走了5.5千米,应付车费多少元?
“为了安全,请勿超速”.如图,一条公路建成通车,在某直线路段MN限速60千米/小时,为了检测车辆是否超速,在公路MN旁设立了观测点C,从观测点C测得一小车从点A到达点B行驶了5秒钟,已知∠CAN=45°,∠CBN=60°,BC=200米,此车超速了吗?请说明理由.(参考数据: ≈1.41,
≈1.41, ≈1.73)
≈1.73)
今年5月,某校为了了解九年级学生的体育备考情况,随机抽取了部分学生进行模拟测试,现将学生按模拟测试成绩m分成A、B、C、D四等(A等:90≤m≤100,B等:80≤m<90,C等:60≤m<80,D等:m<60),并绘制出了如图的两幅不完整的统计图:
(1)本次模拟测试共抽取了多少个学生?
(2)将图乙中条形统计图补充完整;
(3)如果该校今年有九年级学生1000人,试估计其中D等学生的人数.