如图,在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A,交AB于点D,交CA的延长线于点E,过点E作AB的平行线EF交⊙A于点F,连接AF,BF,DF.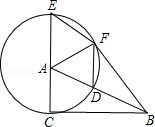
(1)求证:△ABC≌△ABF;
(2)当∠CAB等于多少度时,四边形ADFE为菱形?请给予证明.
已知变量y与变量x之间的对应值如下表:
x … 1 2 3 4 5 6 …
y … 6 3 2 1.5 1.2 1 …
试求出变量y与x之间的函数关系式: .
在生活中不难发现这样的例子:三个量a,b和c之间存在着数量关系a=bc.例如:长方形面积=长×宽,匀速运动的路程=速度×时间.
(1)如果三个量a,b和c之间有着数量关系a=bc,那么:
①当a=0时,必须且只须 ;
②当b(或c)为非零定值时,a与c(或b)之间成 函数关系;
③当a(a≠0)为定值时,b与c之间成 函数关系.
(2)请你编一道有实际意义的应用性问题,解题所列的方程符合数量关系: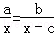 ,(其中x为未知数,a,b,c为已知数,不必解方程).
,(其中x为未知数,a,b,c为已知数,不必解方程).
将x=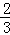 代入反比例函数y=﹣
代入反比例函数y=﹣ 中,所得函数值记为y1,又将x=y1+1代入函数中,所得函数值记为y2,再将x=y2+1代入函数中,所得函数值记为y3,…,如此继续下去.
中,所得函数值记为y1,又将x=y1+1代入函数中,所得函数值记为y2,再将x=y2+1代入函数中,所得函数值记为y3,…,如此继续下去.
(1)完成下表
| y1 |
y2 |
y3 |
y4 |
y5 |
 |
(2)观察上表,你发现了什么规律?猜想y2004= .
已知函数y=2y1﹣y2,y1与x+1成正比例,y2与x成反比例,当x=1时,y=4,当x=2时,y=3,求y与x的函数关系式.
已知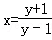 ,若用x表示y,则y= .
,若用x表示y,则y= .