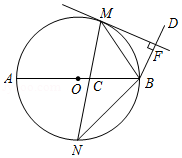
如图, , 是以 为直径的 上的点,且 ,弦 交 于点 , 平分 , 于点 .
(1)求证: 是 的切线;
(2)若 , ,求 的长.
如图,已知在⊙O中,AB、CD是两条弦,且AB⊥CD,于点G,OE⊥BC于点E.
求证:OE= AD.
AD.
如图,AB是⊙O的切线,B为切点,圆心在AC上,∠A=30°,D为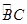 的中点.
的中点.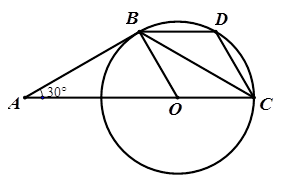
(1)求证:AB=BC;
(2)求证:四边形BOCD是菱形.
如图,M是弧AB的中点,过点M的弦MN交AB于点C,设⊙O的半径为4cm,MN= 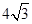 cm.
cm.
(1)求圆心O到弦MN的距离
(2)猜想OM和AB的位置关系,并说明理由。
⊙O的半径为13cm,弦AB∥CD,AB=10cm,CD=24cm.求AB与CD间的距离。
已知:如图,AB是⊙O的直径,AD⊥AB于A, BC⊥AB于B,若∠DOC= 90°.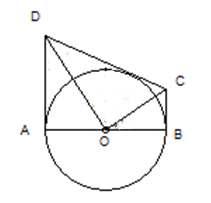
求证:DC是⊙O的切线.