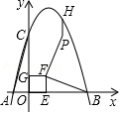
如图,在平面直角坐标系中,抛物线 经过点 和点 ,交 轴正半轴于点 ,连接 ,点 是线段 上一动点(不与点 , 重合),以 为边在 轴上方作正方形 ,连接 ,将线段 绕点 逆时针旋转 ,得到线段 ,过点 作 轴, 交抛物线于点 ,设点 .
(1)求抛物线的解析式.
(2)若 与 相似,求 的值.
(3)当 时,求点 的坐标.
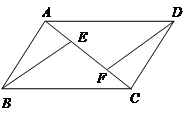
如图, 分别是□ABCD的对角线
分别是□ABCD的对角线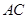 上的两点,且
上的两点,且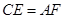 ,求证:
,求证: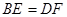
因气候原因,某县城郊外山体引发滑坡,县城居民发现后立即从县城跑步前去救援,此时县政府紧急启动应急预案,一段时间后,公安干警、消防官兵、医疗人员分别乘坐甲、乙、丙三种速度各不相同的车,紧急从县城沿同一线路同时赶往事发地.已知公安、消防、医院分别用5分钟、6分钟、8分钟追上县城救援的居民,且甲车每小时走132km,乙车每小时走112km,则丙车每小时走km
如图,已知:△ABC为边长是 的等边三角形,四边形DEFG为边长是6的正方形.现将等边△ABC和正方形DEFG按如图1的方式摆放,使点C与点E重合,点B、C(E)、F在同一条直线上,△ABC从图1的位置出发,以每秒1个单位长度的速度沿EF方向向右匀速运动,当点C与点F重合时暂停运动,设△ABC的运动时间为t秒(
的等边三角形,四边形DEFG为边长是6的正方形.现将等边△ABC和正方形DEFG按如图1的方式摆放,使点C与点E重合,点B、C(E)、F在同一条直线上,△ABC从图1的位置出发,以每秒1个单位长度的速度沿EF方向向右匀速运动,当点C与点F重合时暂停运动,设△ABC的运动时间为t秒(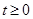 ).
).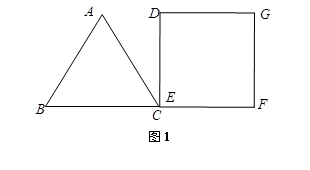
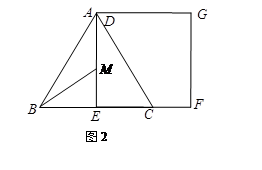
在整个运动过程中,设等边△ABC和正方形DEFG重叠部分的面积为S,请直接写出S与t之间的函数关系式;
如图2,当点A与点D重合时,作
 的角平分线EM交AE于M点,将△ABM绕点A逆时针旋转,使边AB与边AC重合,得到△ACN.在线段AG上是否存在H点,使得△ANH为等腰三角形.如果存在,请求出线段EH的长度;若不存在,请说明理由.
的角平分线EM交AE于M点,将△ABM绕点A逆时针旋转,使边AB与边AC重合,得到△ACN.在线段AG上是否存在H点,使得△ANH为等腰三角形.如果存在,请求出线段EH的长度;若不存在,请说明理由.如图3,若四边形DEFG为边长为
 的正方形,△ABC的移动速度为每秒
的正方形,△ABC的移动速度为每秒 个单位长度,其余条件保持不变.△ABC开始移动的同时,Q点从F点开始,沿折线FG-GD以每秒
个单位长度,其余条件保持不变.△ABC开始移动的同时,Q点从F点开始,沿折线FG-GD以每秒 个单位长度开始移动,△ABC停止运动时,Q点也停止运动.设在运动过程中,DE交折线BA-AC于P点,则是否存在t的值,使得
个单位长度开始移动,△ABC停止运动时,Q点也停止运动.设在运动过程中,DE交折线BA-AC于P点,则是否存在t的值,使得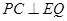 ,若存在,请求出t的值;若不存在,请说明理由
,若存在,请求出t的值;若不存在,请说明理由
2011年11月28日至12月9日,联合国气候变化框架公约第17次缔约方会议在南非德班召开,大会通过了“德班一揽子决议”(DurbanPackageOutcome),建立德班增强行动平台特设工作组,决定实施《京都议定书》第二承诺期并启动绿色气候基金,中国的积极态度赢得与会各国的尊重.
在气候对人类生存压力日趋加大的今天,发展低碳经济,全面实现低碳生活逐渐成为人们的共识.某企业采用技术革新,节能减排. 从去年1至6月,该企业二氧化碳排放量 (吨)与月份x(
(吨)与月份x( ,且x取整数)之间的函数关系如下表:
,且x取整数)之间的函数关系如下表:
| 月份x(月) |
1 |
2 |
3 |
4 |
5 |
6 |
二氧化碳排放量 (吨) (吨) |
600 |
300 |
200 |
150 |
120 |
100 |
去年7至12月,二氧化碳排放量 (吨)与月份x(
(吨)与月份x( ,且x取整数)的变化情况满足二次函数
,且x取整数)的变化情况满足二次函数 ,且去年7月和去年8月该企业的二氧化碳排放量都为56吨.
,且去年7月和去年8月该企业的二氧化碳排放量都为56吨.请观察题中的表格,用所学过的一次函数、反比例函数或二次函数的有关知识,直接写出
 与x之间的函数关系式.并且直接写出
与x之间的函数关系式.并且直接写出 与x之间的函数关系式;
与x之间的函数关系式;政府为了鼓励企业节能减排,决定对每月二氧化碳排放量不超过600吨的企业进行奖励. 去年1至6月奖励标准如下,以每月二氧化碳排放量600吨为标准,不足600吨的二氧化碳排放量每吨奖励
 (元)与月份x满足函数关系式
(元)与月份x满足函数关系式 (
( ,且x取整数),如该企业去年3月二氧化碳排放量为200吨,那么该企业得到奖励的吨数为(
,且x取整数),如该企业去年3月二氧化碳排放量为200吨,那么该企业得到奖励的吨数为( )吨;去年7至12月奖励标准如下:以每月二氧化碳排放量600吨为标准,不足600吨的二氧化碳排放量每吨奖励30元,如该企业去年7月份的二氧化碳排放量为56吨,那么该企业得到奖励的吨数为(
)吨;去年7至12月奖励标准如下:以每月二氧化碳排放量600吨为标准,不足600吨的二氧化碳排放量每吨奖励30元,如该企业去年7月份的二氧化碳排放量为56吨,那么该企业得到奖励的吨数为(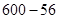 )吨.请你求出去年哪个月政府奖励该企业的资金最多,并求出这个最多资金;
)吨.请你求出去年哪个月政府奖励该企业的资金最多,并求出这个最多资金;在(2)问的基础上,今年1至6月,政府继续加大对节能减排企业的奖励,奖励标准如下:以每月二氧化碳排放量600吨为标准,不足600吨的部分每吨补助比去年12月每吨补助提高m%.在此影响下,该企业继续节能减排,1至3月每月的二氧化碳排放量都在去年12月份的基础上减少24吨.4至6月每月的二氧化碳排放量都在去年12月份的基础上减少m%,若政府今年1至6月奖励给该企业的资金为162000元,请你参考以下数据,估算出 m的整数值.
(参考数据: ,
,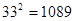 ,
, ,
,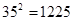 ,
, )
)
如图,在梯形ABCD中, ,
,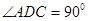 ,过D点作
,过D点作 于E,过B点作
于E,过B点作 交DE于F,连接CF.
交DE于F,连接CF.
若DE平分
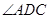 ,DF=2,AD=
,DF=2,AD= ,求
,求
四边形ABFD的面积;若DF=BF,求证:
 .
.