已知:把Rt△ABC和Rt△DEF按如图(1)摆放(点C与点E重合),点B、C(E)、F在同一条直线上.∠ACB =" ∠EDF" = 90°,∠DEF = 45°,AC =" 8" cm,BC =" 6" cm,EF =" 9" cm.
如图(2),△DEF从图(1)的位置出发,以1 cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2 cm/s的速度沿BA向点A匀速移动.当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移动.DE与AC相交于点Q,连接PQ,设移动时间为t(s)(0<t<4.5).解答下列问题: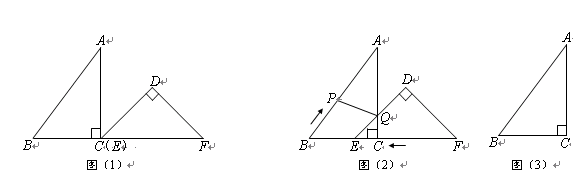
(1)当t为何值时,点A在线段PQ的垂直平分线上?
(2)连接PE,设四边形APEC的面积为y(cm2),求y与t之间的函数关系式;是否存在某一时刻t,使面积y最小?若存在,求出y的最小值;若不存在,说明理由.
(3)是否存在某一时刻t,使P、Q、F三点在同一条直线上?若存在,求出此时t的值;若不存在,说明理由.(图(3)供同学们做题使用)
化简或求值(本题共8分,其中第一小题3分,第二小题5分)
(1)化简:2x2−xy − ( )
)
(2)先化简,再求值:2(xy2+3y3-x2y)-(-2x2y+y3+xy2 )-4y3,其中x=2,y=-3 .
解方程:(每小题4分,共16分)
(1)3-(5-2x)= x+2.
(2)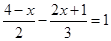
(3)
(4)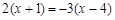
(本题8分)一个不透明的口袋装有若干个红、黄、蓝、绿四种颜色的小球,小球除颜色外完全相同,为估计该口袋中四种颜色的小球数量,每次从口袋中随机摸出一球记下颜色并放回,重复多次试验,汇总实验结果绘制如图不完整的条形统计图和扇形统计图.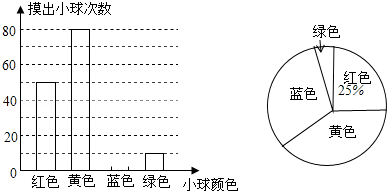
根据以上信息解答下列问题:
(1)求实验总次数,并补全条形统计图;
(2)扇形统计图中,摸到黄色小球次数所在扇形的圆心角度数为多少度?
(3)已知该口袋中有10个红球,请你根据实验结果估计口袋中绿球的数量.
(本题10分)司机在驾驶汽车时,发现紧急情况到踩下刹车需要一段时间,这段时间叫反应时间,之后还会继续行驶一段距离.我们把司机从发现紧急情况到汽车停止所行驶的这段距离叫“刹车距离”(如图).
已知汽车的刹车距离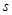 (单位:米)与车速
(单位:米)与车速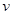 (单位:米/秒)之间有如下关系:
(单位:米/秒)之间有如下关系: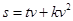 ,其中
,其中 为司机的反应时间(单位:秒),
为司机的反应时间(单位:秒),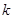 为制动系数.某机构为测试司机饮酒后刹车距离的变化,对某种型号的汽车进行了“醉汉”驾车测试,已知该型号汽车的制动系数
为制动系数.某机构为测试司机饮酒后刹车距离的变化,对某种型号的汽车进行了“醉汉”驾车测试,已知该型号汽车的制动系数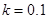 ,并测得志愿者在未饮酒时的反应时间
,并测得志愿者在未饮酒时的反应时间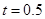 秒.
秒.
(1)若志愿者未饮酒,且车速为10米/秒,则该汽车的刹车距离为 米 ;
(2)当志愿者在喝下一瓶啤酒半小时后,以15米/秒的速度驾车行驶,测得刹车距离为52.5米,此时该志愿者的反应时间是 秒.
(3)假如该志愿者当初是以10米/秒的车速行驶,则刹车距离将比未饮酒时增加多少?
观察下列各式的计算结果:
1-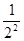 =1-
=1-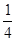 =
=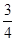 =
=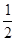 ×
×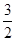 1-
1-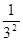 =1-
=1-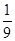 =
=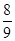 =
=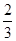 ×
×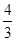
1-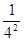 =1-
=1-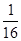 =
=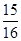 =
=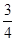 ×
×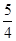 1-
1-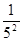 =1-
=1-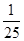 =
=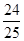 =
= ×
×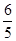 ……
……
(1)用你发现的规律填写下列式子的结果:
1-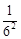 = × ;1-
= × ;1-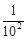 = × ;
= × ;
(2)用你发现的规律计算:
(1-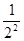 )×(1-
)×(1-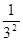 )×(1-
)×(1-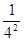 )×…×(1-
)×…×(1-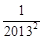 )×(1-
)×(1-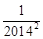 ).
).