（本题10分）司机在驾驶汽车时，发现紧急情况到踩下刹车需要一段时间，这段时间叫反应时间，之后还会继续行驶一段距离．我们把司机从发现紧急情况到汽车停止所行驶的这段距离叫“刹车距离”（如图）．
已知汽车的刹车距离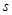
（单位：米）与车速
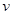（单位：米/秒）之间有如下关系：
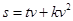，其中
为司机的反应时间（单位：秒），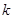
为制动系数．某机构为测试司机饮酒后刹车距离的变化，对某种型号的汽车进行了“醉汉”驾车测试，已知该型号汽车的制动系数
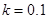，并测得志愿者在未饮酒时的反应时间
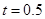秒．
（1）若志愿者未饮酒，且车速为10米/秒，则该汽车的刹车距离为 米 ；
（2）当志愿者在喝下一瓶啤酒半小时后，以15米/秒的速度驾车行驶，测得刹车距离为52.5米，此时该志愿者的反应时间是 秒．
（3）假如该志愿者当初是以10米/秒的车速行驶，则刹车距离将比未饮酒时增加多少？
我们已经学习了一元二次方程的四种解法：因式分解法，开平方法，配方法和公式法．请从以下一元二次方程中任选一个，并选择你认为适当的方法解这个方程．
①
；②
；③
；④
．
计算：
如图①，正方形
的顶点
的坐标分别为
，顶点
在第一象限．点
从点
出发，沿正方形按逆时针方向匀速运动，同时，点
从点
出发，沿
轴正方向以相同速度运动．当点到达点
时，
两点同时停止运动，设运动的时间为
秒．
（1）求正方形的边长．
（2）当点在
边上运动时，
的面积
（平方单位）与时间（秒）之间的函数图象为抛物线的一部分（如图②所示），求两点的运动速度．
（3）求（2）中面积（平方单位）与时间（秒）的函数关系式及面积取最大值时点的坐标．
（4）若点保持（2）中的速度不变，则点沿着边运动时，
的大小随着时间的增大而增大；沿着
边运动时，的大小随着时间的增大而减小．当点沿着这两边运动时，使
的点有 个．
（抛物线
的顶点坐标是
．）
小张骑车往返于甲、乙两地，距甲地的路程
（千米）与时间
（小时）的函数图象如图所示．
（1）小张在路上停留 小时，他从乙地返回时骑车的速度为 千米／时．
（2）小李与小张同时从甲地出发，按相同路线匀速前往乙地，到乙地停止，途中小李与小张共相遇3次．请在图中画出小李距甲地的路程（千米）与时间（小时）的函数的大致图象．
（3）小王与小张同时出发，按相同路线前往乙地，距甲地的路程（千米）与时间（小时）的函数关系式为
．小王与小张在途中共相遇几次？请你计算第一次相遇的时间．
如图，在
中，
为
边上一点，且
．
（1）求证：
．
（2）若
平分
，
，求
的度数．