已知抛物线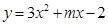
． 
（1）求证：无论
为任何实数，抛物线与x轴总有两个交点；
（2）若为整数，当关于x的方程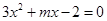
的两个有理数根都在
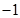与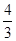
之间（不包括-1、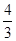）时，求的值．
（3）在（2）的条件下，将抛物线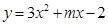在x轴下方的部分沿x轴翻折，图象的其余部分保持不变，得到一个新图象
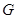，再将图象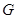向上平移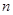
个单位，若图象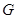与过点（0，3）且与x轴平行的直线有4个交点，直接写出n的取值范围是 ．
已知，关于x，y的方程组
的解满足x＞y＞0．
（1）求a的取值范围；
（2）化简|a|-|2-a|．
如图，在△ABC中，∠B＞∠C，AD⊥BC，垂足为D，AE平分∠BAC．
（1）已知∠B=60°，∠C=30°，求∠DAE的度数；
（2）已知∠B=3∠C，求证：∠DAE=∠C．
小明有1元和5角的硬币共15枚，其中1元的硬币不少于2枚，这些硬币的总币值少于10元．问小明可能有几枚1元的硬币？
看图填空：
已知：如图，AD⊥BC于D，EF⊥BC于F，交AB于G，交CA延长线于E，∠1=∠2．求证：AD平分∠BAC．
证明：∵AD⊥BC，EF⊥BC（已知）
∴∠ADC=90°，∠EFC=90°（垂线的定义）
∴ =
∥
∴∠1=
∠2=
∵∠1=∠2（已知）
∴=
∴AD平分∠BAC（角平分线定义）
解不等式：1-
＜