如果三角形三边的长 、 、 满足 ,那么我们就把这样的三角形叫做“匀称三角形”,如:三边长分别为1,1,1或3,5,7, 的三角形都是“匀称三角形”.
(1)如图1,已知两条线段的长分别为 、 .用直尺和圆规作一个最短边、最长边的长分别为 、 的“匀称三角形”(不写作法,保留作图痕迹);
(2)如图2, 中, ,以 为直径的 交 于点 ,过点 作 的切线交 延长线于点 ,交 于点 ,若 ,判断 是否为“匀称三角形”?请说明理由.
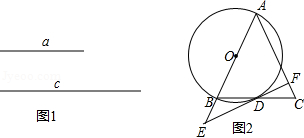
有一长为240米的圆形跑道,小明和他的小狗同时从跑道的点P处出发沿顺时针方向跑步.已知小明的速度为4米/秒,小狗的速度为12米/秒.跑步的时间记为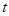 秒.在跑步过程中,小明和他的小狗之间相距(取两者之间较短一段圆弧跑道的长度)为
秒.在跑步过程中,小明和他的小狗之间相距(取两者之间较短一段圆弧跑道的长度)为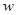 米.
米.
(1)当 秒和
秒和 秒时,分别求
秒时,分别求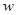 的值?
的值?
(2)当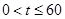 时,请用含
时,请用含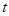 的代数式表示
的代数式表示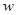 .
.
(3)当 时,请用含
时,请用含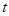 的代数式表示
的代数式表示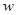 .(可直接写出结果)
.(可直接写出结果)
某空调器销售商,今年四月份销出空调 台,五月份销售空调比四月份的2倍多1台,六月份销售空调比前两个月的总和的4倍少15台.
台,五月份销售空调比四月份的2倍多1台,六月份销售空调比前两个月的总和的4倍少15台.
(1)用代数式表示该销售商今年第二季度共销售空调多少台?
(2)当四月份销出空调为111台时,求第二季度销售的空调总数.
阅读:当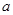 、
、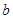 均为正数时,若
均为正数时,若 ,则有
,则有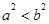 ,反之也成立.
,反之也成立.
活动:现已知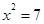 ,请你设计一个方案来确定
,请你设计一个方案来确定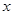 的近似值(精确到小数点后两位).
的近似值(精确到小数点后两位).
观察下列每对数在数轴上的对应点之间的距离:4与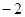 ,3与5,
,3与5,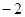 与
与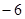 ,
,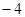 与3.并回答下列各题:
与3.并回答下列各题:
(1)你能发现所得距离与这两个数的差的绝对值有什么关系吗? 答: .
(2)若数轴上的点A表示的数为x,点B表示的数为-1,则A与B两点间的距离可以表示为 .
(3)结合数轴探求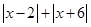 的最小值,并说明取得最小值时x的取值范围.
的最小值,并说明取得最小值时x的取值范围.
某城市大剧院地面的一部分为扇形,观众席的座位按下列方式设置:
| 排数 |
1 |
2 |
3 |
4 |
| 座位数 |
50 |
53 |
56 |
59 |
按这种方式排下去,
(1)第5、6排各有多少个座位?
(2)第n排有多少个座位?
(3)根据(2)的代数式,判断第25排有多少个座位?