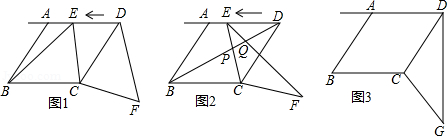
如图1，在菱形 中， ， ，点 从点 出发，以每秒1个单位长度的速度沿着射线 的方向匀速运动，设运动时间为 （秒 ，将线段 绕点 顺时针旋转一个角 ，得到对应线段 ．
（1）求证： ；
（2）当 秒时， 的长度有最小值，最小值等于 ；
（3）如图2，连接 、 、 交 、 于点 、 ，当 为何值时， 是直角三角形？
（4）如图3，将线段 绕点 顺时针旋转一个角 ，得到对应线段 ．在点 的运动过程中，当它的对应点 位于直线 上方时，直接写出点 到直线 的距离 关于时间 的函数表达式．
已知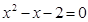
，求代数式
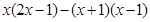的值．
解不等式组：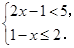
如图，点E，F在线段AC上，AB∥CD，AB＝CD，AE＝CF．求证：BE＝DF．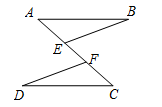
为了节能减排，近期纯电动出租车正式上路运行．某地纯电动出租车的运价为3公里以内10元；超出3公里后每公里2元；单程超过15公里，超过部分每公里3元．小周要到离家10公里的博物馆参观，若他往返都乘坐纯电动出租车，共需付车费元．
数学活动﹣求重叠部分的面积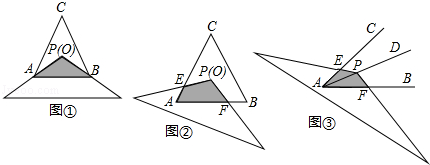
（1）问题情境：如图①，将顶角为120°的等腰三角形纸片（纸片足够大）的顶点P与等边△ABC的内心O重合，已知OA=2，则图中重叠部分△PAB的面积为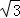
．
（2）探究1：在（1）的条件下，将纸片绕P点旋转至如图②所示位置，纸片两边分别与AC，AB交于点E，F，图②中重叠部分的面积与图①重叠部分的面积是否相等？如果相等，请给予证明；如果不相等，请说明理由．
（3）探究2：如图③，若∠CAB=α（0°＜α＜90°），AD为∠CAB的角平分线，点P在射线AD上，且AP=2，以P为顶点的等腰三角形纸片（纸片足够大）与∠CAB的两边AC，AB分别交于点E、F，∠EPF=180°﹣α，求重叠部分的面积．（用α或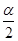
的三角函数值表示）