我们知道,三角形的内心是三条角平分线的交点,过三角形内心的一条直线与两边相交,两交点之间的线段把这个三角形分成两个图形.若有一个图形与原三角形相似,则把这条线段叫做这个三角形的“内似线”.
(1)等边三角形“内似线”的条数为 ;
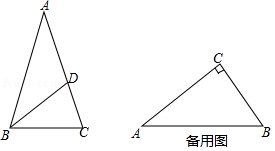
(2)如图, 中, ,点 在 上,且 ,求证: 是 的“内似线”;
(3)在 中, , , , 、 分别在边 、 上,且 是 的“内似线”,求 的长.
如图,在Rt△ABC中, ∠B=90°,AB=3cm,BC=4cm,点P从点A出发, 以1cm/s的速度沿AB运动;同时,点Q从点B出发,以2cm/s的速度沿BC运动,当点Q到达点C时,P、Q两点同时停止运动.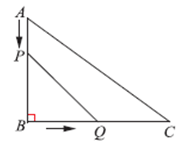
(1)试写出△PBQ的面积S(cm2)与动点运动时间t(s)之间的函数表达式;
(2)运动时间t为何值时,△PBQ的面积等于2cm2?
(3)运动时间t为何值时,△PBQ 的面积S最大?最大值是多少?
已知,如图,扇形AOB的圆心角为120°,半径OA为6cm.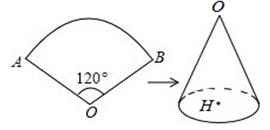
(1)求扇形AOB的弧长和扇形面积;
(2)若把扇形纸片AOB卷成一个圆锥无底纸盒,求这个纸盒的高OH.
某单位招聘员工,采取笔试与面试相结合的方式进行,两项成绩的原始分均为100分.前6名选手的得分如下: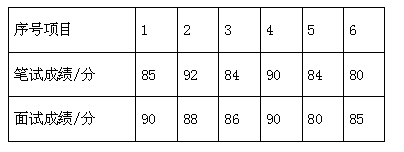
根据规定,笔试成绩和面试成绩分别按一定的百分比折算成综合成绩(综合成绩的满分仍为100分).
(1)求出这6名选手笔试成绩的中位数、众数;
(2)现得知1号选手的综合成绩为88分,求笔试成绩和面试成绩各占的百分比;
(3)求出其余五名选手的综合成绩,并以综合成绩排序确定前两名人选.
已知:如图,AB为⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于 点E,∠BAC=45°.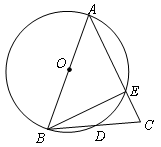
(1)∠EBC求的度数;
(2)求证:BD=CD.
在一个不透明的布口袋中装有只有颜色不同,其他都相同的白、红、黑三种颜色的小球各 只,甲、乙两人进行 摸球游戏:甲先从袋中摸出一球,看清颜色后放回,再由乙从袋中摸出一球.
(1)试用树状图(或列表法)表示摸球游戏所有可能的结果;
(2)如果规定:乙摸到与甲相同颜色的球为乙胜,否则为甲胜,问谁在游戏中获胜的可能性更大些?