某种机器使用期为三年，买方在购进机器时，可以给各台机器分别一次性额外购买若干次维修服务，每次维修服务费为2000元．每台机器在使用期间，如果维修次数未超过购机时购买的维修服务次数，每次实际维修时还需向维修人员支付工时费500元；如果维修次数超过购机时购买的维修服务次数，超出部分每次维修时需支付维修服务费5000元，但无需支付工时费．某公司计划购买1台该种机器，为决策在购买机器时应同时一次性额外购买几次维修服务，搜集并整理了100台这种机器在三年使用期内的维修次数，整理得下表；
维修次数 |
8 |
9 |
10 |
11 |
12 |
频数（台数） |
10 |
20 |
30 |
30 |
10 |
（1）以这100台机器为样本，估计“1台机器在三年使用期内维修次数不大于10”的概率；
（2）试以这100台机器维修费用的平均数作为决策依据，说明购买1台该机器的同时应一次性额外购10次还是11次维修服务？
解不等式组
，并将解集在数轴上表示出来．
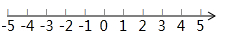
计算：
．
（本小题满分10分）某家电销售商城电冰箱的销售价为每台2100元，空调的销售价为每台1750元，每台电冰箱的进价比每台空调的进价多400元，商城用80000元购进电冰箱的数量与用64000元购进空调的数量相等．
（1）求每台电冰箱与空调的进价分别是多少？
（2）现在商城准备一次购进这两种家电共100台，设购进电冰箱x台，这100台家电的销售总利润为y元，要求购进空调数量不超过电冰箱数量的2倍，总利润不低于13000元，请分析合理的方案共有多少种？并确定获利最大的方案以及最大利润；
（3）实际进货时，厂家对电冰箱出厂价下调k（0＜k＜100）元，若商店保持这两种家电的售价不变，请你根据以上信息及（2）问中条件，设计出使这100台家电销售总利润最大的进货方案．
（本小题满分7分）计算：
．
李明准备进行如下操作实验：把一根长40cm的铗丝剪成两段，并把每段首尾相连各围成一个正方形．
（1）要使这两个正方形的面积之和等于58
，李明应该怎么剪这根铁丝？
（2）李明认为这两个正方形的面积之和不可能等于48．你认为他的说法正确吗？请说明理由．