如图,一次函数 的图象交 轴于点 、交 轴于点 , 的平分线交 轴于点 ,过点 作直线 ,垂足为点 ,交 轴于点 .
(1)求直线 的解析式;
(2)在线段 上有一动点 (不与点 , 重合),过点 分别作 轴, 轴,垂足为点 、 ,是否存在点 ,使线段 的长最小?若存在,请直接写出点 的坐标;若不存在,请说明理由.

已知二次函数y=a(x-m)2-2a(x-m)(a,m为常数,且a≠0).
(1)求证:不论a与m为何值,该函数的图象与x轴总有两个公共点;
(2)设该函数的图象的顶点为C,与x轴交于A,B两点,当△ABC是等腰直角三角形时,求a的值.
阅读理解:
如图1,若在四边形ABCD的边AB上任取一点E(点E与点A,B不重合),分别连结ED,EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的相似点;如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的强相似点.解决问题:
(1)如图1,若∠A=∠B=∠DEC=55°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图2,在矩形ABCD中,AB=5,BC=2,且A,B,C,D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图2中画出矩形ABCD的边AB上的一个强相似点E;
拓展探究:
(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处.若点E恰好是四边形ABCM的边AB上的一个强相似点,请直接写出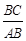 的值.
的值.
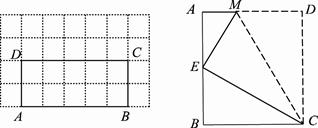
图1图2图3
在Rt△ACB中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,且∠CBD=∠A.
(1)判断直线BD与⊙O的位置关系,并证明你的结论;
(2)若AD∶AO=8∶5,BC=3,求BD的长.
在一幅长8分米,宽6分米的矩形风景画(如图①)的四周镶宽度相同的金色纸边,制成一幅矩形挂图(如图②).如果要使整个挂图的面积是80平方分米,求金色纸边的宽.
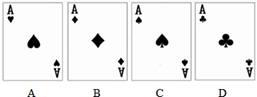
如图,有四张背面相同的纸牌A,B,C,D,其正面分别是红桃、方块、黑桃、梅花,其中红桃、方块为红色,黑桃、梅花为黑色.小明将这4张纸牌背面朝上洗匀后,摸出一张,将剩余3张洗匀后再摸出一张.请用画树状图或列表的方法求摸出的两张牌均为黑色的概率.