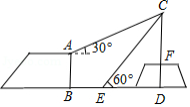
如图， 是某景区内高 的观景台， 是与 底部相平的一座雕像（含底座），在观景台顶 处测得雕像顶 点的仰角为 ，从观景台底部 处向雕像方向水平前进 到达点 ，在 处测得雕像顶 点的仰角为 ，已知雕像底座 高 ，求雕像 的高．（结果保留根号）
已知实数a满足
，求
的值．
解不等式组
．
如图，AB=AD，AC=AE，∠CAD=∠EAB．求证：BC=DE．
某中学库存若干套桌椅，准备修理后支援贫困山区学校。现有甲、乙两木工组，甲每天修理桌椅16套，乙每天修桌椅比甲多8套，甲单独修完这些桌椅比乙单独修完多用20天，学校每天付甲组80元修理费，付乙组120元修理费。
(1)该中学库存多少套桌椅？
(2)在修理过程中，学校要派一名工人进行质量监督，学校负担他每天10元生活补助费，现有三种修理方案:a、由甲单独修理；b、由乙单独修理；c、甲、乙合作同时修理。你认为哪种方案省时又省钱？为什么？
请阅读下列材料：让我们来规定一种运算：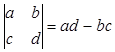
，例如：
=2×5－3×4=10－12=－2. 按照这种运算的规定，若
=
，试用方程的知识求x的值。