如图,以 的边 为直径的 交 边于点 ,交 边于点 ,连接 ,过点 的切线交 的延长线于点 , .
(1)求证: 为等腰三角形.
(2)求证: .

一块矩形纸片,利用割补的办法可以拼成一块与它面积相等的平行四边形(如图1所示):
请你根 据图1作法的提示,利用图2画出一个平行四边形,使该平行四边形的面积等于所给的矩形面积.
据图1作法的提示,利用图2画出一个平行四边形,使该平行四边形的面积等于所给的矩形面积.
要求:(1)画出的平行四边形有且只有一个顶点与B点重合;
(2)写出画图步骤;
(3)写出所画的平行四边形的名称.
2010年5月20日上午10时起,2010年广州亚运会门票全面发售.下表为抄录广州亚运会官方网公布的三类比赛的部分门票价格,下图为某公司购买的门票种类、数量所绘制成的条形统计图.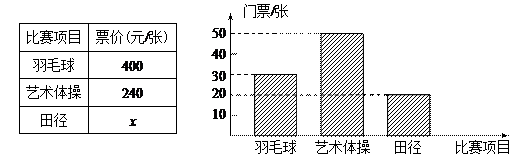
依据上面的表和图,回答下列问题:
(1)其中观看羽毛球比赛的门票有张;观看田径比赛的门票占全部门票的 %.
(2)公司决定采用随机抽取的方式把门票分配给部分员工,在看不到门票的条件下,每人抽取一张(假设所有的门票形状、大小、质地等完全相同且充分洗匀 ),问员工小丽抽到艺术体操门票的概率是.
),问员工小丽抽到艺术体操门票的概率是.
(3)若该公司购买全部门票共花了36000元,试求每张田径门票的价格.
如图,在边长为1的正方形网格内,点A、B、C、D、E均在格点处.请你判断∠x+∠y的度数,并加以证明.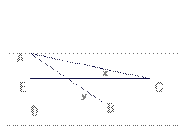
已知:如图,在直角梯形ABCD中,AD∥BC,∠A=90°,∠C=45°,上底AD = 8,AB=12,CD边的垂直平分线交BC边于点G,且交AB的延长线于点E,求AE的长.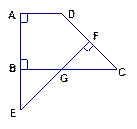
在平面直角坐标系中,点A的坐标是(0,6),点B在一次函数y=-x+m的图象上,且AB=OB=5.求一次函数的解析式.