如图，在边长为1的正方形网格内，点A、B、C、D、E均在格点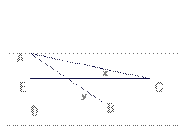-优题课

已知：如图，抛物线 $y = a x^{2} + bx + c$ 与坐标轴分别交于点 $A (0, 6)$ ， $B (6, 0)$ ， $C (- 2, 0)$ ，点 $P$ 是线段 $AB$ 上方抛物线上的一个动点．

（1）求抛物线的解析式；

（2）当点 $P$ 运动到什么位置时， $ΔPAB$ 的面积有最大值？

（3）过点 $P$ 作 $x$ 轴的垂线，交线段 $AB$ 于点 $D$ ，再过点 $P$ 做 $PE / / x$ 轴交抛物线于点 $E$ ，连接 $DE$ ，请问是否存在点 $P$ 使 $ΔPDE$ 为等腰直角三角形？若存在，求出点 $P$ 的坐标；若不存在，说明理由．

已知：如图，在 $Rt Δ ABC$ 中， $∠ ACB = 90 °$ ，点 $M$ 是斜边 $AB$ 的中点， $MD / / BC$ ，且 $MD = CM$ ， $DE ⊥ AB$ 于点 $E$ ，连接 $AD$ 、 $CD$ ．

（1）求证： $ΔMED ∽ ΔBCA$ ；

（2）求证： $ΔAMD ≅ ΔCMD$ ；

（3）设 $ΔMDE$ 的面积为 $S_{1}$ ，四边形 $BCMD$ 的面积为 $S_{2}$ ，当 $S_{2} = \frac{17}{5} S_{1}$ 时，求 $\cos ∠ ABC$ 的值．

如图是小红在一次放风筝活动中某时段的示意图，她在 $A$ 处时的风筝线（整个过程中风筝线近似地看作直线）与水平线构成 $30 °$ 角，线段 $A A_{1}$ 表示小红身高1.5米．

（1）当风筝的水平距离 $AC = 18$ 米时，求此时风筝线 $AD$ 的长度；

（2）当她从点 $A$ 跑动 $9 \sqrt{2}$ 米到达点 $B$ 处时，风筝线与水平线构成 $45 °$ 角，此时风筝到达点 $E$ 处，风筝的水平移动距离 $CF = 10 \sqrt{3}$ 米，这一过程中风筝线的长度保持不变，求风筝原来的高度 $C_{1} D$ ．

已知：如图，在 $ΔABC$ 中， $AB = AC$ ，点 $P$ 是底边 $BC$ 上一点且满足 $PA = PB$ ， $⊙ O$ 是 $ΔPAB$ 的外接圆，过点 $P$ 作 $PD / / AB$ 交 $AC$ 于点 $D$ ．

（1）求证： $PD$ 是 $⊙ O$ 的切线；

（2）若 $BC = 8$ ， $\tan ∠ ABC = \frac{\sqrt{2}}{2}$ ，求 $⊙ O$ 的半径．

为了美化市容市貌，政府决定将城区旁边一块162亩的荒地改建为湿地公园，规划公园分为绿化区和休闲区两部分．

（1）若休闲区面积是绿化区面积的 $20 %$ ，求改建后的绿化区和休闲区各有多少亩？

（2）经预算，绿化区的改建费用平均每亩35000元，休闲区的改建费用平均每亩25000元，政府计划投入资金不超过550万元，那么绿化区的面积最多可以达到多少亩？