为了美化市容市貌,政府决定将城区旁边一块162亩的荒地改建为湿地公园,规划公园分为绿化区和休闲区两部分.
(1)若休闲区面积是绿化区面积的 ,求改建后的绿化区和休闲区各有多少亩?
(2)经预算,绿化区的改建费用平均每亩35000元,休闲区的改建费用平均每亩25000元,政府计划投入资金不超过550万元,那么绿化区的面积最多可以达到多少亩?
先化简,再求值: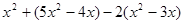 (其中
(其中 )
)
某商店经销一种销售成本为每千克40元的水产品.据市场分析,若按每千克50元销售,一个月能售出500kg;销售单价每涨1元,月销售量就减少10kg.针对这种水产品的销售情况,请解答以下问题:
(1)当销售单价定为每千克55元时,计算月销售量和月销售利润;
(2)设销售单价为每千克x元,月销售利润为y元,求y与x的函数关系式;
(3)商店想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应定为多少?
如图,⊙O是△ABC的外接圆,AB为直径,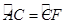 ,CD⊥AB于D,且交⊙O于G,AF交CD于E.
,CD⊥AB于D,且交⊙O于G,AF交CD于E.
(1)求∠ACB的度数;
(2)求证:AE=CE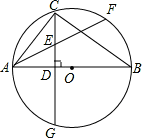
在一不透明的口袋中装有3个球,这3个球分别标有1,2,3,这些球除了数字外都相同.
(1)如果从袋子中任意摸出一个球,那么摸到标有数字是2的球的概率是多少?
(2)小明和小亮玩摸球游戏,游戏的规则如下:先由小明随机摸出一个球,记下球的数字后 放回,搅匀后再由小亮随机摸出一个球,记下数字.谁摸出的球的数字大 ,谁获胜.请你用树状图或列 表法分析游戏规则对双方是否公平?并说明理由.
下图是输水管的切面,阴影部分是有水部分,其中水面AB宽16㎝,水最深4㎝,求这个圆形切面的半径.