在平面直角坐标系 中， 抛物线 的开口向上， 且经过点
（1） 若此抛物线经过点 ，且与 轴相交于点 ， ．
①填空： （用 含 的代数式表示） ；
②当 的值最小时， 求抛物线的解析式；
（2） 若 ，当 ，抛物线上的点到 轴距离的最大值为 3 时， 求 的值 ．
阅读下面的材料：
小明遇到一个问题：如图（1），在□ABCD中，点E是边BC的中点，点F是线段AE上一点，BF的延长线交射线CD于点G.如果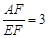
，求
的值.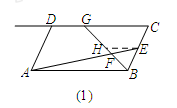 
他的做法是：过点E作EH∥AB交BG于点H，则可以得到△BAF∽△HEF.
请你回答：（1）AB和EH的数量关系为，CG和EH的数量关系为，的值为.
（2）如图（2），在原题的其他条件不变的情况下，如果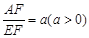
，那么的值为（用含a的代数式表示）.
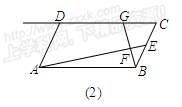
（3）请你参考小明的方法继续探究：如图（3），在四边形ABCD中，DC∥AB，点E是BC延长线上一点，AE和BD相交于点F. 如果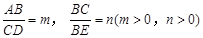
，那么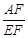
的值为（用含m，n的代数式表示）.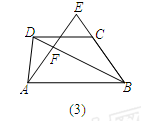
已知：如图，在△ABC中，AB=AC，以AC为直径的⊙O与BC交于点D，DE⊥AB，垂足为E，ED的延长线与AC的延长线交于点F.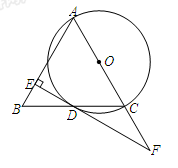
（1）求证：DE是⊙O的切线；
（2）若⊙O的半径为4，BE=2，求∠F的度数.
（1）已知二次函数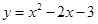
，请你化成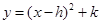
的形式，并在直角坐标系中画出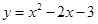的图象；
（2）如果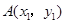
，
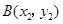是（1）中图象上的两点，且
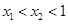，请直接写出
、
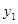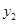的大小关系；
（3）利用（1）中的图象表示出方程
的根来，要求保留画图痕迹，说明结果．
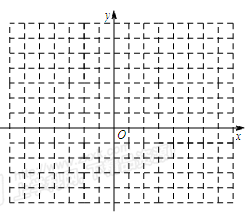
如图，在平面直角坐标系
中，⊙A与y轴相切于点
，与x轴相交于M、N两点.如果点M的坐标为
，求点N的坐标.
如图，在△ABC中，∠ABC=2∠C，BD平分∠ABC，且
，
，求AB的值.