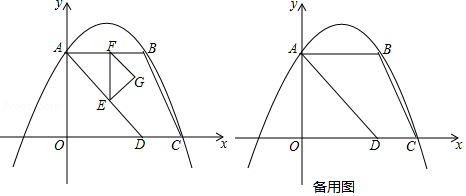
如图,抛物线 交 轴于点 ,并经过 和 两点,点 的坐标为 ,连接 , , ,点 从点 出发,以每秒 个单位长度的速度沿线段 向点 运动,到达点 后,以每秒1个单位长度的速度沿射线 运动,设点 的运动时间为 秒,过点 作 的垂线 交直线 于点 ,以线段 为斜边向右作等腰直角 .
(1)求抛物线的解析式;
(2)当点 落在第一象限内的抛物线上时,求出 的值;
(3)设点 从点 出发时,点 , , 都与点 重合,点 在运动过程中,当 的面积为4时,直接写出相应的 值,并直接写出点 从出发到此时所经过的路径长.
如图,∠BAD=∠CAE=90o,AB=AD,AE=AC,AF⊥CF,垂足为F.
(1)若AC=10,求四边形ABCD的面积;
(2)求证:AC平分∠ECF;
(3)求证:CE="2AF" .
如图,在△ABC中,∠BCA=90º,CA=CB,AD为BC边上的中线,CG⊥AD于G,交AB于F,过点B作BC的垂线交CG于E.求证:∠ADC=∠BDF.
一辆汽车开往距离出发地180千米的目的地,出发后第一小时内按原计划的速度匀速行驶,一小时后以原来速度的1.5倍匀速行驶,并比原计划提前40分钟到达目的地,求原计划的行驶速度.
如图,已知BD为△ABC的中线,CE⊥BD于E,AF⊥BD于F.求证:BE+BF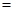 2BD
2BD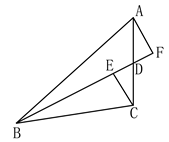
已知关于x的方程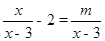 的解是正数,求m的取值范围.
的解是正数,求m的取值范围.