如图,在某建筑物AC上,挂着宣传条幅BC,小明站在点F处,看条幅顶端B,测得的仰角为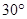 ,再往条幅方向前行20米到达点E处,看条幅顶端B,测得的仰角为
,再往条幅方向前行20米到达点E处,看条幅顶端B,测得的仰角为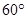 ,若小明的身高约1.7米,求宣传条幅BC的长(结果精确到1米)。
,若小明的身高约1.7米,求宣传条幅BC的长(结果精确到1米)。
如图,已知抛物线 过点 , , ,点 、 为抛物线上的动点,过点 作 轴,交直线 于点 ,交 轴于点 .
(1)求二次函数 的表达式;
(2)过点 作 轴,垂足为点 ,若四边形 为正方形(此处限定点 在对称轴的右侧),求该正方形的面积;
(3)若 , ,求点 的横坐标.

如图,四边形 为一个矩形纸片, , ,动点 自 点出发沿 方向运动至 点后停止, 以直线 为轴翻折,点 落在点 的位置.设 ,△ 与原纸片重叠部分的面积为 .

(1)当 为何值时,直线 过点 ?
(2)当 为何值时,直线 过 的中点 ?
(3)求出 与 的函数表达式.
已知: 为 的直径, ,弦 ,直线 与 相交于点 ,弦 在 上运动且保持长度不变, 的切线 交 于点 .
(1)如图1,若 ,求证: ;
(2)如图2,当点 运动至与点 重合时,试判断 与 是否相等,并说明理由.

图1是太阳能热水器装置的示意图.利用玻璃吸热管可以把太阳能转化为热能,玻璃吸热管与太阳光线垂直时,吸收太阳能的效果最好,假设某用户要求根据本地区冬至正午时刻太阳光线与地面水平线的夹角 确定玻璃吸热管的倾斜角(太阳光线与玻璃吸热管垂直),请完成以下计算:
如图2, ,垂足为点 , ,垂足为点 , , , , ,垂足为点 .
(1)若 ,则 的长约为 ;
(参考数据: , ,
(2)若 , ,求 的长.

央视热播节目“朗读者”激发了学生的阅读兴趣.某校为满足学生的阅读需求,欲购进一批学生喜欢的图书,学校组织学生会成员随机抽取部分学生进行问卷调查,被调查学生须从“文史类、社科类、小说类、生活类”中选择自己喜欢的一类,根据调查结果绘制了统计图(未完成),请根据图中信息,解答下列问题:
(1)此次共调查了 名学生;
(2)将条形统计图补充完整;
(3)图2中“小说类”所在扇形的圆心角为 度;
(4)若该校共有学生2500人,估计该校喜欢“社科类”书籍的学生人数.
