如图,四边形 为一个矩形纸片, , ,动点 自 点出发沿 方向运动至 点后停止, 以直线 为轴翻折,点 落在点 的位置.设 ,△ 与原纸片重叠部分的面积为 .

(1)当 为何值时,直线 过点 ?
(2)当 为何值时,直线 过 的中点 ?
(3)求出 与 的函数表达式.
近日某小区计划在中央花园内建造一个圆形的喷水池,在水池中央垂直于水面安装一个花形柱子OA,O恰好在水面中心,OA为1.25m,安置在柱子顶端A处的喷头向外喷水,水流在各个方向上沿形状相同的抛物线路径落下,且在过OA的任一平面上抛物线路径如图所示.为使水流形状较为漂亮,设计成水流在到OA距离lm处达到距水面最大高度2.25m.
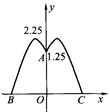
(1)请求出其中一条抛物线的解析式;
(2)如果不计其他因素,那么水池的半径至少要为多少m 才能使喷出水流不致落到池上?
如图,P是⊙O的直径AB延长线上的一点, PC切⊙O于点C,弦CD⊥AB,垂足为点E,若 ,
,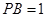 .
.
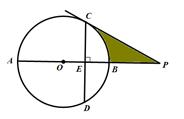
求:(1)⊙O的半径;
(2)CD的长;
(3)图中阴影部分的面积.
已知:抛物线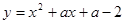 .
.
(1)求证:不论a取何值时,抛物线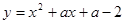 与x轴都有两个不同的交点.
与x轴都有两个不同的交点.
(2)设这个二次函数的图象与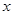 轴相交于A(
轴相交于A(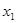 ,0),B(
,0),B(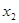 ,0),且
,0),且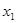 、
、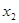 的平方和为3,求a的值.
的平方和为3,求a的值.
已知二次函数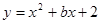 的图像经过点(-1,6)
的图像经过点(-1,6)
(1)求这个二次函数的关系式;
(2)求二次函数图像与x轴的交点的坐标;
(3)画出图像的草图,观察图像,直接写出当y>0时,x的取值范围.
分别求出对应的二次函数的解析式:
(1)已知抛物线的顶点为(-2,1),且过点(-4,3);
(2)抛物线与x轴的两个交点坐标为(-3,0)和(2,0),且它经过点(1,4).