如图，∠MAN60°，AP平分∠MAN，点B是射线AP上一定-优题课

题文

如图， $∠ MAN = 60 °$ ， $AP$ 平分 $∠ MAN$ ，点 $B$ 是射线 $AP$ 上一定点，点 $C$ 在直线 $AN$ 上运动，连接 $BC$ ，将 $∠ ABC (0 ° < ∠ ABC < 120 °)$ 的两边射线 $BC$ 和 $BA$ 分别绕点 $B$ 顺时针旋转 $120 °$ ，旋转后角的两边分别与射线 $AM$ 交于点 $D$ 和点 $E$ ．

（1）如图1，当点 $C$ 在射线 $AN$ 上时，

①请判断线段 $BC$ 与 $BD$ 的数量关系，直接写出结论；

②请探究线段 $AC$ ， $AD$ 和 $BE$ 之间的数量关系，写出结论并证明；

（2）如图2，当点 $C$ 在射线 $AN$ 的反向延长线上时， $BC$ 交射线 $AM$ 于点 $F$ ，若 $AB = 4$ ， $AC = \sqrt{3}$ ，请直接写出线段 $AD$ 和 $DF$ 的长．

科目数学题型解答题难度中等

知识点：相似三角形的判定与性质几何变换综合题全等三角形的判定与性质

登录免费查看答案和解析

相关试题

如图，梯形ABCD中，AD∥BC，BC＝20cm，AD＝10cm，现有两个动点P、Q
分别从B、D两点同时出发，点P以每秒2cm的速度沿BC向终点C移动，点Q以每秒1cm
的速度沿DA向终点A移动，线段PQ与BD相交于点E，过E作EF∥BC交CD于点F，射线
QF交BC的延长线于点H，设动点P、Q移动的时间为t（单位：秒，0<t<10）．
（1）当t为何值时，四边形PCDQ为平行四边形？
（2）在P、Q移动的过程中，线段PH的长是否发生改变？如果不变，求出线段PH的长；如果改变，请说明理由．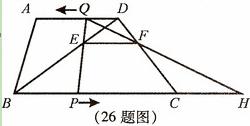

“六·一”儿童节前，某玩具商店根据市场调查，用2500元购进一批儿童玩
具，上市后很快脱销，接着又用4500元购进第二批这种玩具，所购数量是第一批数量的1.5
倍，但每套进价多了10元．
（1）求第一批玩具每套的进价是多少元？
（2）如果这两批玩具每套售价相同，且全部售完后总利润不低于25%，那么每套售价至少是多少元？

有四张卡片（背面完全相同），分别写有数字1、2、-1、-2，把它们背面朝
上洗匀后，甲同学抽取一张记下这个数字后放回洗匀，乙同学再从中抽出一张，记下这个
数字，用字母b、c分别表示甲、乙两同学抽出的数字．
（1）用列表法求关于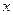的方程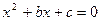有实数解的概率；
（2）求（1）中方程有两个相等实数解的概率．

(10分) 把一张矩形ABCD纸片按如图方式折叠，使点A与点E重合，点C与点F重合（E、F两点均在BD上），折痕分别为BH、DG．
（1）求证：△BHE≌△DGF；
（2）若AB＝6cm，BC＝8cm，求线段FG的长．

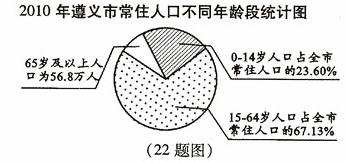
(10分))第六次全国人口普查工作圆满结束，2011年5月20日《遵义晚报》报到了遵义市人口普查结果，并根据我市常住人口情况，绘制出不同年龄段的扇形统计图；普查结果显示，2010年我市常住人口中，每10万人就有4402人具有大学文化程度，与2000年第五次人口普查相比，是2000年每10万人具有大学文化程度人数的3倍少473人，请根据以上信息，解答下列问题．
（1）65岁及以上人口占全市常住人口的百分比是▲；
（2）我市2010年常住人口约为▲万人（结果保留四个有效数字）；
（3）与2000年我市常住人口654.4万人相比，10年间我市常住人口减少▲万人；
（4）2010年我市每10万人口中具有大学文化程度人数比2000年增加了多少人？

试卷网试题网古诗词网作文网范文网