为了解某校九年级学生的身高情况，随机抽取部分学生的身高进行调-优题课

题文

为了解某校九年级学生的身高情况，随机抽取部分学生的身高进行调查，利用所得数据绘成如图统计图表：

频数分布表

身高分组	频数	百分比
$x < 155$	5	$10 %$
$155 ⩽ x < 160$	$a$	$20 %$
$160 ⩽ x < 165$	15	$30 %$
$165 ⩽ x < 170$	14	$b$
$x ⩾ 170$	6	$12 %$
总计		$100 %$

（1）填空： $a =$ 　　， $b =$ 　　；

（2）补全频数分布直方图；

（3）该校九年级共有600名学生，估计身高不低于 $165 cm$ 的学生大约有多少人？

科目数学题型解答题难度中等

知识点：用样本估计总体频数（率）分布表频数（率）分布直方图

登录免费查看答案和解析

相关试题

如图，在正方形ABCD中，点E、F分别在BC和CD上，AE=AF．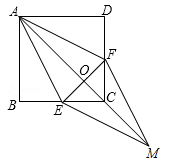

（1）求证：BE=DF
（2）连接AC交EF于点D，延长OC至点M，使OM=OA，连结EM、FM，试证明四边形AEMF是菱形．

如图，一次函数y₁=mx+n的图象与x轴、y轴分别交于A、B两点，与反比例函数y₂=（x＜0）交于点C，过点C分别作x轴、y轴的垂线，垂足分别为点E、F．若OB=2，CF=6，．

（1）求点A的坐标；
（2）求一次函数和反比例函数的表达式．

某商店第一次用6000元购进了练习本若干本，第二次又用6000元购进该款练习本，但这次每本进货的价格是第一次进货价格的1.2倍，购进数量比第一次少了1000本．
（1）问：第一次每本的进货价是多少元？
（2）若要求这两次购进的练习本按同一价格全部销售完毕后获利不低于4500元，问每本售价至少是多少元？

如图，在△ABC中，AD是角平分钱，点E在AC上，且∠EAD=∠ADE．

（1）求证：△DCE∽△BCA；
（2）若AB=3，AC=4．求DE的长．

在一个布口袋里装着白、红、黑三种颜色的小球，它们除颜色之外没有任何其它区别，其中有白球3只、红球2只、黑球1只．袋中的球已经搅匀．
（1）闭上眼睛随机地从袋中取出1只球，求取出的球是黑球的概率；
（2）若取出的第1只球是红球，将它放在桌上，闭上眼睛从袋中余下的球中再随机地取出1只球，这时取出的球还是红球的概率是多少？
（3）若取出一只球，将它放回袋中，闭上眼睛从袋中再随机地取出1只球，两次取出的球都是白球概率是多少？（用列表法或树状图法计算）

试卷网试题网古诗词网作文网范文网