如今很多初中生购买饮品饮用，既影响身体健康又给家庭增加不必要的开销，为此数学兴趣小组对本班同学一天饮用饮品的情况进行了调查，大致可分为四种：
：自带白开水； ：瓶装矿泉水； ：碳酸饮料； ：非碳酸饮料．
根据统计结果绘制如下两个统计图，根据统计图提供的信息，解答下列问题：
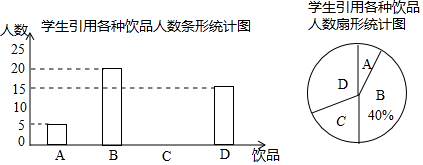
（1）这个班级有多少名同学？并补全条形统计图．
（2）若该班同学每人每天只饮用一种饮品（每种仅限1瓶，价格如下表），则该班同学用于饮品上的人均花费是多少元？
饮品名称 |
自带白开水 |
瓶装矿泉水 |
碳酸饮料 |
非碳酸饮料 |
平均价格（元 瓶） |
0 |
2 |
3 |
4 |
（3）若我市约有初中生4万人，估计我市初中生每天用于饮品上的花费是多少元？
（4）为了养成良好的生活习惯，班主任决定在自带白开水的5名同学（男生2人，女生3人）中随机抽取2名同学做良好习惯监督员，请用列表法或树状图法求出恰好抽到2名女生的概率．
如图，△ABC中，∠C=Rt∠，AB=10cm，BC=6cm，若动点P从点C开始，按C→A→B→C的路径运动，且速度为每秒1cm，设出发的时间为t秒．
（1）出发2秒后，求△ABP的周长．
（2）问t为何值时，△BCP为等腰三角形？
（3）另有一点Q，从点C开始，按C→B→A→C的路径运动，且速度为每秒2cm，若P、Q两点同时出发，当P、Q中有一点到达终点时，另一点也停止运动．当t为何值时，直线PQ把△ABC的周长分成相等的两部分？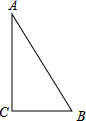
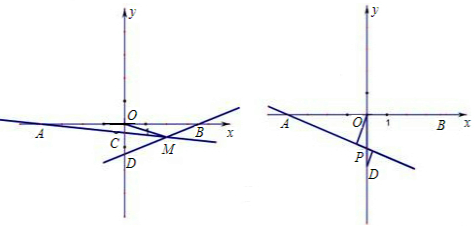
如左图：直线y=kx+4k（k≠0）交x轴于点A，交y轴于点C，点M（2，m）为直线AC上一点，过点M的直线BD交x轴于点B，交y轴于点D．
（1）求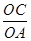
的值（用含有k的式子表示．）；
（2）若S△BOM=3S△DOM，且k为方程（k+7）（k+5）﹣（k+6）（k+5）=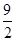
的根，求直线BD的解析式．
（3）如右图，在（2）的条件下，P为线段OD之间的动点（点P不与点O和点D重合），OE上AP于E，DF上AP于F，下列两个结论：①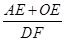
值不变；②
值不变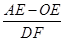，请你判断其中哪一个结论是正确的，并说明理由并求出其值．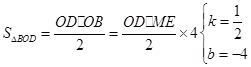
．
如图，直线y=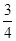
x+6与x轴、y轴分别相交于点E、F，点A的坐标为（﹣6，0），P（x，y）是直线y=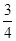x+6上一个动点．
（1）在点P运动过程中，试写出△OPA的面积s与x的函数关系式；
（2）当P运动到什么位置，△OPA的面积为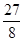
，求出此时点P的坐标；
（3）过P作EF的垂线分别交x轴、y轴于C、D．是否存在这样的点P，使△COD≌△FOE？若存在，直接写出此时点P的坐标（不要求写解答过程）；若不存在，请说明理由．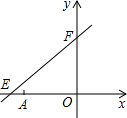
已知：如图，平面直角坐标系xOy中，点A、B的坐标分别为A（4，0），B（0，﹣4），P为y轴上B点下方一点，PB=m（m＞0），以AP为边作等腰直角三角形APM，其中PM=PA，点M落在第四象限．
（1）求直线AB的解析式；
（2）用m的代数式表示点M的坐标；
（3）若直线MB与x轴交于点Q，判断点Q的坐标是否随m的变化而变化，写出你的结论并说明理由．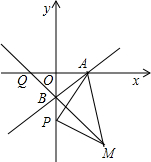
如图，将边长为4的正方形置于平面直角坐标系第一象限，使AB边落在x轴正半轴上，且A点的坐标是（1，0）．
（1）直线
经过点C，且与x轴交于点E，求四边形AECD的面积；
（2）若直线l经过点E，且将正方形ABCD分成面积相等的两部分，求直线l的解析式；
（3）若直线l1经过点F（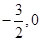
）且与直线y=3x平行．将（2）中直线l沿着y轴向上平移1个单位，交x轴于点M，交直线l1于点N，求△NMF的面积．