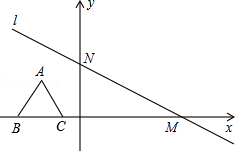
如图，在平面直角坐标系中，直线l:y−33x4与x轴、y轴分-优题课

题文

如图，在平面直角坐标系中，直线 $l : y = - \frac{\sqrt{3}}{3} x + 4$ 与 $x$ 轴、 $y$ 轴分别交于点 $M$ ， $N$ ，高为3的等边三角形 $ABC$ ，边 $BC$ 在 $x$ 轴上，将此三角形沿着 $x$ 轴的正方向平移，在平移过程中，得到△ $A_{1} B_{1} C_{1}$ ，当点 $B_{1}$ 与原点重合时，解答下列问题：

（1）求出点 $A_{1}$ 的坐标，并判断点 $A_{1}$ 是否在直线 $l$ 上；

（2）求出边 $A_{1} C_{1}$ 所在直线的解析式；

（3）在坐标平面内找一点 $P$ ，使得以 $P$ 、 $A_{1}$ 、 $C_{1}$ 、 $M$ 为顶点的四边形是平行四边形，请直接写出 $P$ 点坐标．

科目数学题型解答题难度中等

知识点：平行四边形的判定与性质待定系数法求一次函数解析式一次函数综合题

登录免费查看答案和解析

相关试题

利达经销店为某工厂代销一种建筑材料．当每千克售价为260元时，月销售量为45千克．该经销店为提高经营利润，准备采取降价的方式进行促销．经市场调查发现：当每千克售价下降10元时，月销售量就会增加5千克．综合考虑各种因素，每售出一千克建筑材料共需支付厂家及其它费用100元．设每千克材料售价为x（元），该经销店的月利润为y（元）．
（1）当每千克售价是240元时，计算此时的月销售量；
（2）求出y与x的函数关系式（不要求写出x的取值范围）；
（3）该经销店要获得最大月利润，售价应定为每千克多少元?

如图，在△ABC中，AB=AC，以AB为直径作半圆⊙0，交BC于点D，连接AD，过点D作DE⊥AC，垂足为点E，交AB的延长线于点F．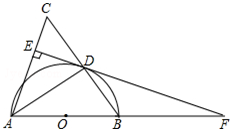

（1）求证：EF是⊙0的切线;
（2）如果⊙0的半径为9，sin∠ADE=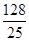，求AE的长．

如图，矩形ABCD中，AB=20，BC=10，点P为AB边上一动点，DP交AC于点Q．

（1）求证：△APQ∽△CDQ；
（2）P点从A点出发沿AB边以每秒1个单位长度的速度向B点移动，移动时间为t秒．当t为何值时，DP⊥AC？

某文具店老板第一次用1000元购进一批文具，很快销售完毕；第二次购进时发现每件文具进价比第一次上涨了2 5元。老板用2500元购进了第二批文具，所购进文具的数量是第一次购进数量的2倍，同样很快销售完毕，两批文具的售价均为每件15元。
（1）问第二次购进了多少件文具？
（2）文具店老板第一次购进的文具有3% 的损耗，第二次购进的文具有5% 的损耗，问文具店老板在这两笔生意中是盈利还是亏本？请说明理由。

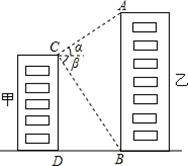
如图，甲、乙两栋高楼的水平距离BD为90米，从甲楼顶部C点测得乙楼顶部A点的仰角α为30°，测得乙楼底部B点的俯角β为60°，求甲、乙两栋高楼各有多高？（计算过程和结果都不取近似值）

试卷网试题网古诗词网作文网范文网