如图， 中， 为钝角， ，点 是边 延长线上一点，以点 为顶点， 为边，在射线 下方作 ．
（1）在射线 上取点 ，连接 交线段 于点 ．
①如图1，若 ，请直接写出线段 与 的数量关系和位置关系；
②如图2，若 ，判断线段 与 的数量关系和位置关系，并说明理由；
（2）如图3，反向延长射线 ，交射线 于点 ，将 沿 方向平移，使顶点 落在点 处，记平移后的 为 ，将 绕点 顺时针旋转角 ， 交线段 于点 ， 交射线 于点 ，请直接写出线段 ， 与 之间的数量关系．
某地的一种绿色蔬菜，在市场上若直接销售，每吨利润为1000元，经粗加工后销售，每吨利润4000元，经精加工后销售，每吨利润7000元。当地一家公司现有这种蔬菜140吨，该公司加工厂的生产能力是：如果对蔬菜进行粗加工，每天可加工16吨，如果对蔬菜进行精加工，每天可加工6吨，但每天两种方式不能同时进行．受季节等条件的限制，必须用15天时间将这批蔬菜全部销售或加工完毕．为此，公司研制了三种方案：
方案一：将蔬菜全部进行粗加工；
方案二：尽可能地对蔬菜进行精加工，没来得及加工的蔬菜，在市场上直接出售；
方案三：将一部分蔬菜进行精加工，其余蔬菜进行粗加工，并刚好15天完成．
如果你是公司经理，你会选择哪一种方案，说说理由．
甲、乙两人登一座山，甲每分钟登高10米，并且先出发30分钟，乙每分钟登高15米，两人同时登上山顶．甲用多少时间登山？这座山有多高？
如图6,已知∠BOC=2∠AOB,OD平分∠AOC,∠BOD=14°,求∠AOB的度数．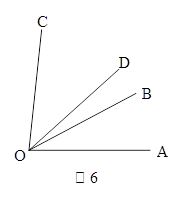
某出租车一天下午以A点为出发地在东西方向营运，向东走为正，向西走为负，行车里程（单位：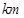
）依先后次序记录如下：
，
，
，
，
，
，，
，
，
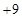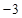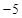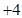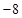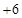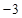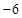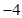．将最后一名乘客送到目的地，出租车离出发地点A多远？在点A的什么方向？
若每千米的价格为2.4元，司机一个下午的营业额是多少？
解方程：