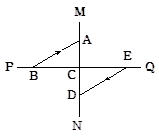如图, 的对角线 、 相交于点 , 过点 且与 、 分别相交于点 、 ,连接 .
(1)求证: ;
(2)若 , 的周长是10,求 的周长.
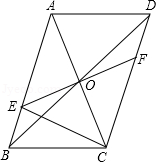
分解因式: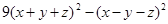
分解因式:
我们知道,两边及其中一边的对角分别对应相等的两个三角形不一定全等. 那么在什么情况下,它们会全等?
(1)阅读与证明:
对于这两个三角形均为直角三角形,显然它们全等.
对于这两个三角形均为钝角三角形,可证它们全等(证明略).
对于这两个三角形均为锐角三角形,它们也全等,可证明如下:
已知:△ABC、△A1B1C1均为锐角三角形,AB=A1B1,BC=B1C1,∠C=∠C1.
求证:△ABC≌△A1B1C1. (请你将下列证明过程补充完整)
证明:分别过点B,B1作BD⊥CA于D,B1D1⊥C1A1于D1.
则∠BDC=∠B1D1C1=90°,
∵BC=B1C1,∠C=∠C1,
∴△BCD≌△B1C1D1,
∴BD=B1D1.
______________________________。
(2)归纳与叙述:
由(1)可得到一个正确结论,请你写出这个结论. 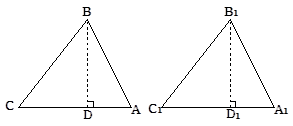
有一块不规则的鱼池,下面是两位同学分别设计的能够粗略地测量出鱼池两端A、B的距离的方案,请你分析一下两种方案的理由.
方案一:小明想出了这样一个方法,如图①所示,先在AB的垂线BF上取两点C、D,使CD=BC,再定出BF的垂线DE,使A、C、E在同一条直线上,测得DE的长就是AB的长. 你能说明一下这是为什么吗?
方案二:小军想出了这样一个方法,如图②所示,先在平地上取一个可以直接到达鱼池两端A、B的点C,连结AC并延长到点D,使CD=CA,连结BC并延长到E,使CE=CB,连结DE,量出DE的长,这个长就是A、B之间的距离. 你能说明一下这是为什么吗?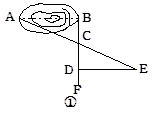
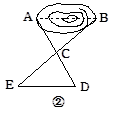
MN、PQ是校园里的两条互相垂直的小路,小强和小明分别站在距交叉口C等距离的B、E两处,这时他们分别从B、E两点按同一速度沿直线行走,如图所示,经过一段时间后,同时到达A、D两点,他们的行走路线AB、DE平行吗?请说明你的理由.