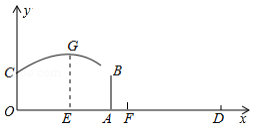
为备战2016年里约奥运会，中国女排的姑娘们刻苦训练，为国争光，如图，已知排球场的长度 为18米，位于球场中线处球网的高度 为2.43米，一队员站在点 处发球，排球从点 的正上方1.8米的 点向正前方飞出，当排球运行至离点 的水平距离 为7米时，到达最高点 建立如图所示的平面直角坐标系．
（1）当球上升的最大高度为3.2米时，求排球飞行的高度 （单位：米）与水平距离 （单位：米）的函数关系式．（不要求写自变量 的取值范围）．
（2）在（1）的条件下，对方距球网0.5米的点 处有一队员，他起跳后的最大高度为3.1米，问这次她是否可以拦网成功？请通过计算说明．
（3）若队员发球既要过球网，又不出边界，问排球飞行的最大高度 的取值范围是多少？（排球压线属于没出界）
某中学课外活动小组准备围建一个矩形生物苗圃园，其中一边靠墙，另外三边用长为30米的篱笆围成，已知墙长为18米。设这个苗圃园垂直于墙的一边的长为x米
（1）用含x的代数式表示平行于墙的一边的长为＿＿＿＿米，.x的取值范围为＿＿＿＿
（2）这个苗圃园的面积为88平方米时，求x的值
如图，在□ABCD中，E，F分别为边AB，CD的中点，连结DE，BF，BD．
（1）求证：△ADE≌△CBF．
（2）若AD⊥BD，则四边形BFDE是什么特殊四边形?请证明你的结论．
如图，已知点A（-4，8）和点B（2，n）在抛物线
上．求a的值及点B的坐标.
已知关于x的一元二次方程x2+2x+m=0．
（1）当m=3时，判断方程的根的情况；
（2）当m=-3时，求方程的根．
试说明关于
的方程
无论
取何值，该方程都是一元二次方程。