小颖在学习“两点之间线段最短”查阅资料时发现: 内总存在一点 与三个顶点的连线的夹角相等,此时该点到三个顶点的距离之和最小.
【特例】如图1,点 为等边 的中心,将 绕点 逆时针旋转 得到 ,从而有 ,连接 得到 ,同时 , ,即 、 、 、 四点共线,故 .在 中,另取一点 ,易知点 与三个顶点连线的夹角不相等,可证明 、 、 、 四点不共线,所以 ,即点 到三个顶点距离之和最小.

【探究】(1)如图2, 为 内一点, ,证明 的值最小;
【拓展】(2)如图3, 中, , , ,且点 为 内一点,求点 到三个顶点的距离之和的最小值.
如图,已知 的直径 ,弦 , 是 的中点,过点 作 ,交 的延长线于点 .
(1)求证: 是 的切线;
(2)求 的长.

某商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量 (单位:个)与销售单价 (单位:元)有如下关系: .
设这种双肩包每天的销售利润为 元.
(1)求 与 之间的函数解析式;
(2)这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?
为了参加学校举行的传统文化知识竞赛,某班进行了四次模拟训练,将成绩优秀的人数和优秀率绘制成如下两个不完整的统计图:
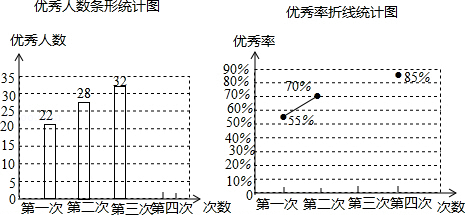
请根据以上两图解答下列问题:
(1)该班总人数是 ;
(2)根据计算,请你补全两个统计图;
(3)观察补全后的统计图,写出一条你发现的结论.
如图1,矩形 的顶点 , 的坐标分别为 , ,直线 交 于点 , ,抛物线 过 , 两点.
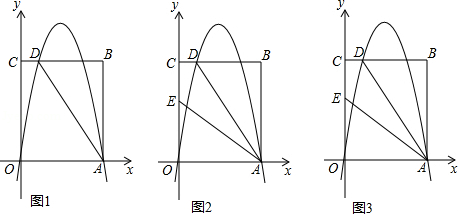
(1)求点 的坐标和抛物线 的表达式;
(2)点 是抛物线 对称轴上一动点,当 时,求所有符合条件的点 的坐标;
(3)如图2,点 ,连接 ,将抛物线 的图象向下平移 个单位得到抛物线 .
①设点 平移后的对应点为点 ,当点 恰好在直线 上时,求 的值;
②当 时,若抛物线 与直线 有两个交点,求 的取值范围.
某学习小组的学生在学习中遇到了下面的问题:
如图1,在
和
中,
,
,点
,
,
在同一条直线上,连接
,点
是
的中点,连接
,
,试判断
的形状并说明理由.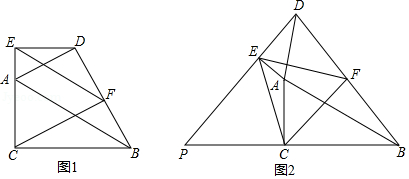
问题探究:
(1)小婷同学提出解题思路:先探究 的两条边是否相等,如 ,以下是她的证明过程
|
证明:延长线段 交 的延长线于点 . 是 的中点, . , . |
. 又 , . . . |
请根据以上证明过程,解答下列两个问题:
①在图1中作出证明中所描述的辅助线;
②在证明的括号中填写理由(请在 , , , 中选择).
(2)在(1)的探究结论的基础上,请你帮助小婷求出 的度数,并判断 的形状.
问题拓展:
(3)如图2,当 绕点 逆时针旋转某个角度时,连接 ,延长 交 的延长线于点 ,其他条件不变,判断 的形状并给出证明.